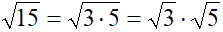PRODOTTO TRA RADICALI
- Radicali di indice n
- Radicali con indice dispari
- Condizione di esistenza dei radicali
- Operazioni con i radicali
- L'insieme dei numeri naturali
- Simboli usati per l'insieme dei numeri naturali
- L'insieme dei numeri reali
Iniziamo ad occuparci delle OPERAZIONI con i RADICALI partendo dal PRODOTTO DI RADICALI.
Dati due radicali, aventi lo STESSO INDICE n, con n appartenente ai numeri NATURALI e DIVERSO DA ZERO, il loro PRODOTTO è un RADICALE che ha:
- per indice lo STESSO INDICE dei radicali dati;
- per radicando il PRODOTTO dei RADICANDI dati.
Ovviamente, dobbiamo sempre porre la condizione che:
- se n è PARI, a e b devono essere MAGGIORI o UGUALI a ZERO;
- se n è DISPARI, è sufficiente che a e b appartengano ai REALI.
In altre parole:
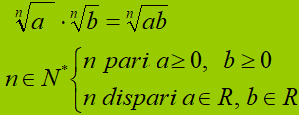
che si legge
il prodotto della radice ennesima di a per la radice ennesima di b
è uguale
alla radice ennesima di a per b
con
n appartenente ad enne asterisco (ovvero l'insieme dei numeri naturali escluso lo zero)
e,
se n è pari con a maggiore o uguale a zero e b maggiore o uguale a zero
se n è dispari con a appartenente ai reali e b appartenente ai reali.
Dimostriamo la regola che abbiamo appena enunciato.
Sappiamo che un radicale può essere indicato come potenza con esponente frazionario, quindi:
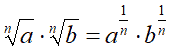
Applicando le proprietà delle potenze possiamo scrivere:
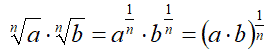
Ma, sempre ricorrendo alle potenze con esponente frazionario, possiamo scrivere:
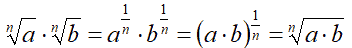
Quindi possiamo dire che:
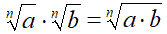
Facciamo alcuni esempi.
Indice dispari: è sufficiente che a e b appartengano ai reali.
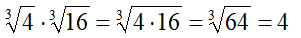
Indice pari: è necessario che a e b siano positivi o uguali a zero.
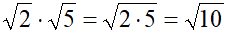
Indice dispari: è sufficiente che a e b appartengano ai reali.
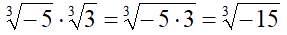
Questa l'avremmo potuta risolvere anche così:
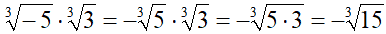
La regola appena vista presuppone che i radicali da moltiplicare abbiamo lo STESSO INDICE. Pertanto, nel caso si debbano moltiplicare tra loro radicali con INDICE DIVERSO, è necessario dapprima RIDURRE I RADICALI allo STESSO INDICE e successivamente procedere come abbiamo appena visto.
Inoltre la regola vale anche nel caso del PRODOTTO di TRE o PIU' RADICALI aventi lo stesso indice.
Ovviamente, per la proprietà simmetrica dell'uguaglianza, possiamo anche scrivere che:
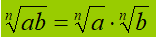
ponendo sempre attenzione alle condizioni di esistenza dei radicali.
Esempio: