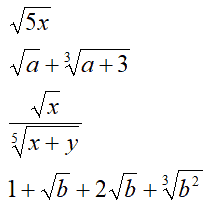CONDIZIONI DI ESISTENZA DEI RADICALI
- Radicali di indice n
- L'insieme dei numeri reali
- Frazioni algebriche
- I monomi
- Campo di esistenza di una frazione algebrica
- Disequazioni fratte
- Rappresentazione delle soluzioni di una disequazione
Immaginiamo di avere un RADICALE, il cui RADICANDO contenta una o più LETTERE. Esempio:
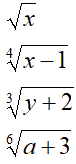
Parliamo di CONDIZIONI DI ESISTENZA di un radicale, per intendere le condizioni che devono essere soddisfatte dai NUMERI REALI RAPPRESENTATI dalle LETTERE che compaiono nel radicando, affinché il radicale abbia significato.
La CONDIZIONE di ESISTENZA si indica con la sigla
C.E.
Per determinare le condizioni di esistenza di un radicale occorre distinguere due casi:
- nel caso in cui l'INDICE è PARI, la condizione di esistenza è che il RADICANDO sia POSITIVO o UGUALE A ZERO. Sappiamo, infatti, che non si può estrarre una radice di indice pari se il radicando è negativo;
- nel caso in cui l'INDICE è DISPARI, non vi è NESSUNA condizione di esistenza particolare dato che, il radicando può assumere qualsiasi valore (negativo, nullo o positivo), quindi è sufficiente che l'incognita appartenga ai reali.
Tornando agli esempi precedenti avremo:
| RADICALE | INDICE | CONDIZIONE DI ESISTENZA |
|---|---|---|
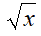 |
PARI | x ≥ 0 |
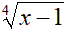 |
PARI | x - 1 ≥
0
x ≥ 1 |
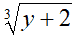 |
DISPARI | 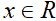 |
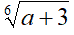 |
PARI | a + 3 ≥
0
a ≥ -3 |
E se nel radicando vi sono delle FRAZIONI ALGEBRICHE, cioè frazioni che hanno come numeratore e denominatore due monomi tra loro non divisibili?
In questo caso occorre, oltre alle condizioni di esistenza che abbiamo appena visto, porre anche la CONDIZIONE che il DENOMINATORE sia DIVERSO DA ZERO, affinché la frazione abbia significato.
Esempi:
- INDICE PARI
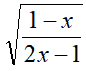
Essendo l'indice pari dobbiamo porre due condizioni:
- la prima che il radicando sia diverso o uguale a zero;
- la seconda che il denominatore sia diverso da zero.
Ovvero
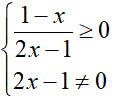
Iniziamo col risolvere la prima disequazione:
Risolviamo separatamente il numeratore e il denominatore.
NUMERATORE:
1 - x ≥ 0
- x ≥ -1
x ≤ 1
DENOMINATORE:
dato che il denominatore deve essere diverso da zero, escludiamo tale caso ponendo nella disequazione, anziché il segno maggiore uguale, solamente maggiore
2x - 1 > 0
2x > 1
x > 1/2.
Rappresentiamo graficamente il risultato del numeratore e del denominatore:
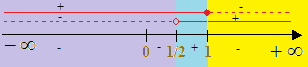
Come possiamo notare la disequazione risulta essere positiva quando
1/2 < x ≤ 1.
Il risultato ottenuto tiene conto anche della condizione che il denominatore sia diverso da zero.
- INDICE
DISPARI
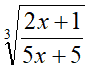
Essendo l'indice dispari dobbiamo porre solamente la condizione che che il denominatore sia diverso da zero.
Quindi
5x + 5 ≠ 0
5x ≠ -5
x ≠ -1.
Quindi la condizione di esistenza è data da tutti i numeri reali escluso -1.
Concludiamo questa lezione dicendo che si chiamano ESPRESSIONI LETTERALI IRRAZIONALI quelle espressione nelle quali compare almeno un RADICALE con RADICANDO ETTERALE. Esempio: