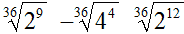RIDUZIONE DI RADICALI ALLO STESSO INDICE
- Proprietà invariantiva dei radicali
- Semplificazione dei radicali
- Semplificazione dei radicali: casi particolari
- Minimo comune multiplo
- Calcolo del minimo comune multiplo
- Divisione
- Scomposizione di un numero in fattori primi
La PROPRIETA' INVARIANTIVA dei RADICALI ci permette di TRASFORMARE due o più radicali in modo che essi abbiano tutti lo STESSO INDICE.
In questo modo potremo:
- CONFRONTARE radicali che hanno indici diversi;
- MOLTIPLICARE o DIVIDERE radicali che hanno indici diversi.
Vediamo come occorre procedere per RIDURRE due o più RADICALI allo STESSO INDICE:
- per prima cosa bisogna SEMPLIFICARE i radicali, nel caso in cui ciò è possibile;
- quindi si deve calcolare il minimo comune multiplo degli indici dei radicali. Tale minimo comune multiplo prende il nome di MINIMO COMUNE INDICE;
- infine
si deve TRASFORMARE ognuno dei
radicali in un altro che abbia come indice il MINIMO
COMUNE INDICE. Per fare ciò si usa la proprietà
invariantiva. In altre parole:
- si DIVIDE il MINIMO COMUNE INDICE per l'INDICE del radicale da trasformare;
- si
MOLTIPLICA il QUOZIENTE
ottenuto:
- sia per l'INDICE del radicale;
- che per l'ESPONENTE del radicando.
Esempio:
vogliamo ridurre, allo stesso indice, i seguenti radicali
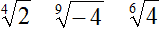
Iniziamo col semplificare i radicali per i quali ciò è possibile.
Il primo radicale non può essere semplificato.
Il secondo radicale non può essere semplificato, ma può essere scritto nel modo seguente:
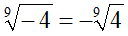
Il terzo radicale può essere semplificato così:
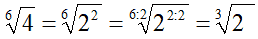
Quindi, i nostri tre radicali, sono diventati:
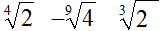
A questo punto calcoliamo il MINIMO COMUNE INDICE, cioè il m.c.m. tra gli indici.
I nostri indici sono
4 , 9 , 3.
Ricordiamo che per calcolare il m.c.m. basta scomporre i numeri in fattori primi e moltiplicare i FATTORI PRIMI COMUNI e NON COMUNI, ciascuno preso una sola volta, col MASSIMO ESPONENTE.
Quindi
4 = 22
9 = 32
3 = 3
m.c.m. (4; 9; 3) = 22 x 32 = 4 x 9 = 36 .
Ora trasformiamo i nostri radicali, in radicali di indice 36.
Prediamo il primo radicale
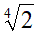
e lo trasformiamo in un radicale di indice 36.
Per fare ciò:
- dividiamo
il minimo comune indice 36 per
l'indice del radicale 4,
in modo da ottenere 9:
36 : 4 = 9;
- moltiplichiamo
il quoziente ottenuto 9 per
l'indice del radicale 4
in modo da avere 36
che sarà l'indice del radicale nel quale andiamo a trasformare quello
precedente
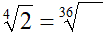
-
moltiplichiamo
il quoziente ottenuto 9 per
l'esponente del radicando 1,
in modo da avere 9
che sarà l'esponente del radicando della nuova radice
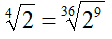
Passiamo al secondo radicale
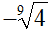
- dividiamo il minimo comune indice 36 per l'indice del radicale 9, in modo da ottenere 4;
- moltiplichiamo il quoziente ottenuto 4, per l'indice del radicale 9 in modo da avere 36 che sarà l'indice del radicale nel quale andiamo a trasformare quello precedente;
- moltiplichiamo
il quoziente ottenuto 4, per
l'esponente del radicando 1
in modo da avere 4
che sarà l'esponente del radicando della nuova radice
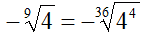
Terminiamo con l'ultimo radicale
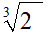
- dividiamo il minimo comune indice 36 per l'indice del radicale 3 in modo da ottenere 12;
- moltiplichiamo il quoziente ottenuto 12 per l'indice del radicale 3, in modo da avere 36 che sarà l'indice del radicale nel quale andiamo a trasformare quello precedente;
- moltiplichiamo
il quoziente ottenuto 12, per
l'esponente del radicando 1
in modo da avere 12
che sarà l'esponente del radicando della nuova radice
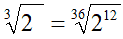
Quindi, i tre radicali
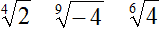
ridotti allo stesso indice, diventano