OPERAZIONI CON I NUMERI IN NOTAZIONE SCIENTIFICA
- Elevamento a potenza
- Casi particolari dell'elevazione a potenza
- Proprietà delle potenze
- Potenze con esponente negativo
Quando ci troviamo di fronte a numeri molto grandi o molto piccoli, capita spesso di scriverli in NOTAZIONE SCIENTIFICA.
Un numero scritto in NOTAZIONE SCIENTIFICA si presenta nel modo seguente:
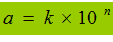
con
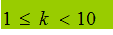
e
n
interno.
Ora può accadere anche di dover eseguire delle OPERAZIONI su numeri scritti in NOTAZIONE SCIENTIFICA.
Iniziamo dalla SOMMA e SOTTRAZIONE di due numeri scritti in NOTAZIONE SCIENTIFICA.
Esempio:
2,5 x 103 + 1,18 x 103.
In questo caso i due numeri da sommare hanno lo STESSO ORDINE DI GRANDEZZA (103).
Quindi è sufficiente mettere in evidenza 103.
Quindi, avremo:
2,5 x 103 + 1,18 x 103 = (2,5 + 1,18) x 103 = 3,68 x 103.
Vediamo, ora, cosa accade se i due numeri NON HANNO LO STESSO ORDINE DI GRANDEZZA.
Esempio:
1,7 x 103 + 2,13 x 105.
In questo caso dobbiamo esprimere tutte e due i numeri nello STESSO ORDINE DI GRANDEZZA: si sceglie, a tal fine, l'ORDINE DI GRANDEZZA DEL NUMERO PIU' GRANDE.
Nel nostro caso il numero più grande è
2,13 x 105.
Quindi scegliamo come ordine di grandezza 105 e scriviamo il primo numero
1,7 x 103
sotto forma di potenza di 105, spostando la virgola verso sinistra di due posti, così:
0,017 x 105.
Ora eseguiamo la somma mettendo in evidenza 105.
0,017 x 105 + 2,13 x 105 = (0,017 + 2,13) x 105 = 2,147 x 105.
Vediamo un altro esempio:
1,56 x 10-2 + 4,7 x 10-3 = 1,56 x 10-2 + 0,47 x 10-2= (1,56 + 0,47) x 10-2 = 2,03 x 10-2.
Chiaramente si procede in modo analogo se, anziché una somma si deve eseguire una sottrazione.
Esempio:
7,3 x 107 - 3,1 x 106 = 7,3 x 107 - 0,31 x 107= (7,3 - 0,31) x 107 = 6,99 x 107.
Se, invece, dobbiamo eseguire una MOLTIPLICAZIONE o una DIVISIONE tra due numeri scritti in NOTAZIONE SCIENTIFICA si applicano le PROPRIETA' DELLA MOLTIPLICAZIONE o della DIVISIONE le PROPRIETA' DELLE POTENZE ovvero:
-
il
prodotto di due o più potenze aventi la stessa base è
una potenza della stessa base con esponente uguale alla
somma degli esponenti.
am x an = a m+n
-
il
quoziente di due o più potenze aventi la stessa base è
una potenza della stessa base con esponente uguale alla
differenza degli esponenti.
am : an = a m-n.
Esempio:
3,8 x 103 x 7,5 x 105 = (3,8 x 7,5) x (103 x 105) = 28,5 x 103+5= 28,5 x 108.
In alcuni casi, come questo, otteniamo un valore di
k >10.
Sarà allora necessario riportare il risultato in NOTAZIONE SCIENTIFICA con k maggiore o uguale a 1 e minore di 10.
28,5 x 108 = 2,85 x 109.
Oppure:
7,31 x 10-15 : 1,15 x 10-5 = (7,31 : 1,15) x (10-15 : 10-5) = 6,3565 x 10-15-(-5) = 6,3565 x 10-15+5= 6,3565 x 10-10.
Per eseguire la POTENZA di un numero scritto in NOTAZIONE SCIENTIFICA si esegue la POTENZA DELLA PARTE NUMERICA e la POTENZA DEL 10 e, se necessario, si riporta il risultato in NOTAZIONE SCIENTIFICA con k maggiore o uguale a 1 e minore di 10.
Ricordiamo che la potenza di una potenza è una potenza che ha per base la stessa base e per esponente il prodotto degli esponenti.
(am)n = a mn.
Esempio:
(2,5 x 103)2 = 2,52 x 103x2 = 6,25 x 106.
- Ordine di grandezza di un numero
- Notazione scientifica di un numero
- Notazione scientifica e ordine di grandezza di un numero






