DOMINIO DI UNA FUNZIONE LOGARITMICA
- Funzioni reali di variabile reale
- Classificazione delle funzioni reali
- Funzione logaritmica
- L'insieme dei numeri reali
- Elevamento a potenza
Se poniamo:
ax = b
che si legge
a elevato ad x uguale b
possiamo affermare che
x = loga b
che si legge
x è uguale al logaritmo in base a di b.
Chiamiamo:
- a BASE del logaritmo;
- b ARGOMENTO del logaritmo.
Poniamo come condizione che:
- a sia POSITIVO e DIVERSO da 1;
- b sia POSITIVO.
Queste condizioni sono necessarie affinché il logaritmo esista e sia unico.
Vediamo il perché:
- a deve essere POSITIVO perché con la base negativa non avremmo sempre risultati reali;
- a deve essere DIVERSO da 1 perché se a = 1, qualunque sia il valore di x, b è sempre uguale ad 1;
- b deve essere POSITIVO perché se a è positivo non esiste un numero x per il quale viene elevato a che dia un risultato negativo.
Poste queste premesse chiamiamo FUNZIONE LOGARITMICA una funzione nella quale la variabile x compare come argomento di un logaritmo. Essa si presenta normalmente nel modo seguente:
y = log x
che si legge
y uguale logaritmo di x.
Poiché abbiamo detto che l'ARGOMENTO DEL LOGARITMO deve essere MAGGIORE DI ZERO, il CAMPO DI ESISTENZA della funzione sarà dato da:
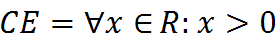
che si legge
campo di esistenza è uguale ad ogni x appartenente ai reali tale che x è maggiore di zero.
Esempio:
y = log x.
Quindi il campo di esistenza è dato dall'insieme di tutti i numeri reali maggiori di zero.
Un altro tipo di FUNZIONE LOGARITMICA è la seguente:
y = log P(x)
che si legge
y è uguale al logaritmo di P con x.
Anche in questo caso dobbiamo porre la condizione che l'ARGOMENTO del logaritmo sia MAGGIORE di zero. Quindi il CAMPO DI ESISTENZA della funzione sarà dato da tutti i valori di x per i quali P(x) è maggiore di zero. Quindi:
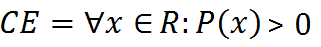
che si legge
campo di esistenza è uguale ad ogni x appartenente ai reali tali che P con x è maggiore di zero.
Esempio:
y = log (x - 2).
Il campo di esistenza della funzione è dato da
x - 2 > 0
ovvero
x > 2.






