ESEMPI SUL TEOREMA DI PITAGORA
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Esempi di applicazione del teorema di Pitagora
- Le formule inverse del teorema di Pitagora
- Triangolo rettangolo
- Perimetro di un poligono
Nella lezione precedente abbiamo visto le FORMULE INVERSE del TEOREMA DI PITAGORA: esse ci permettono di trovare la misura di un cateto del triangolo rettangolo conoscendo la misura dell'altro cateto e dell'ipotenusa.
Proviamo ad applicare le formule viste in precedenza ad alcuni casi concreti.
Esempio 1:
un triangolo rettangolo ha l'ipotenusa e uno dei cateti lunghi rispettivamente cm 7 e cm 4. Determinare la lunghezza dell'altro cateto.
Applichiamo la formula seguente:
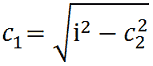
Andiamo a sostituire i nostri valori e avremo:

Il cateto misura cm 5,74.
Esempio 2:
calcolare il perimetro di un triangolo rettangolo che ha l'ipotenusa lunga cm 3,4 e un cateto lungo cm 1,5.
Per poter calcolare il perimetro del triangolo dobbiamo prima sapere quanto misurano tutti i suoi lati. Ora noi conosciamo la misura dell'ipotenusa e di un cateto: dobbiamo trovare quanto misura l'altro cateto. Quindi:

Il cateto cercato misura cm 3,05.
Quindi il perimetro è uguale a:
P = cm 3,4 + cm 1,5 + cm 3,05 = cm 7,95.






