ESEMPI DI APPLICAZIONE DEL TEOREMA DI PITAGORA
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Triangolo rettangolo
- Perimetro di un poligono
Nella lezione precedente abbiamo visto che, applicando il TEOREMA DI PITAGORA possiamo trovare l'ipotenusa di un triangolo rettangolo conoscendo la misura dei due cateti.
Basterà applicare la seguente formula:
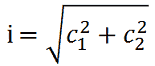
dove
i = ipotenusa
c1 = un cateto
c2 = l'altro cateto.
Vediamo come fare in pratica.
Esempio 1:
calcolare la misura dell'ipotenusa di un triangolo rettangolo i cui cateti misurano rispettivamente m 6 e m 6,5.
Sarà sufficiente applicare la formula precedente, per cui avremo:

L'ipotenusa misura m 8,85.
Esempio 2:
calcolare il perimetro di un triangolo rettangolo i cui cateti misurano rispettivamente cm 4 e cm 9.
Per trovare il perimetro del triangolo dobbiamo conoscere la misura di tutti i suoi lati. Poiché già conosciamo la misura dei due cateti ci rimane da trovare la misura dell'ipotenusa. Essa è data da:

L'ipotenusa misura cm 9,85.
Quindi il perimetro sarà dato da:
p = cm 4 + cm 9 + cm 9,85 = cm 22,85.






