AREA DEL CERCHIO
- Lunghezza della circonferenza
- La circonferenza e il cerchio
- Quadrato
- Quadrilateri inscritti
- I poligoni
- Poligoni regolari inscritti
- Area di un poligono regolare
- Semplificazione di una frazione
Disegniamo una CIRCONFERENZA di raggio r
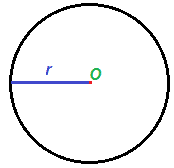
Ora disegniamo dapprima il QUADRATO INSCRITTO alla circonferenza, successivamente l'ESAGONO REGOLARE INSCRITTO ed infine l'OTTAGONO REGOLARE INSCRITTO.
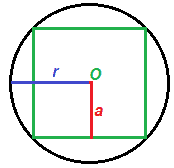
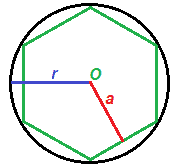

Osserviamo i lati dei POLIGONI INSCRITTI: il lato dell'esagono è minore rispetto al lato del quadrato e il lato dell'ottagono è minore rispetto al lato dell'esagono.
Possiamo allora affermare che il LATO di un POLIGONO REGOLARE INSCRITTO in una circonferenza DIMINUISCE all'AUMENTARE del numero dei SUOI LATI.
Quindi, possiamo immaginare di INSCRIVERE in un cerchio un POLIGONO REGOLARE con un NUMERO INFINITO di LATI in modo tale che questi diventino così piccoli da non distinguersi dalla circonferenza ad esso circoscritta.
Osserviamo ora l'APOTEMA dei poligoni inscritti, che nell'immagine sopra abbiamo indicato con la lettera a: l'apotema dell'esagono è maggiore rispetto all'apotema del quadrato e l'apotema dell'ottagono è maggiore rispetto all'apotema dell'esagono.
Possiamo allora affermare che l'APOTEMA di un POLIGONO REGOLARE INSCRITTO in una circonferenza CRESCE all'AUMENTARE del numero dei SUOI LATI.
Se INSCRIVIAMO in un cerchio un POLIGONO REGOLARE con un NUMERO INFINITO di LATI l'APOTEMA CRESCE al punto da AVVICINARSI sempre più al RAGGIO della circonferenza ad esso circoscritta.
Per queste ragioni possiamo considerare il CERCHIO come un POLIGONO INSCRITTO IN ESSO avente un NUMERO ELEVATISSIMO di LATI. In questo modo:
- il PERIMETRO di tale poligono tende a coincidere con la CIRCONFERENZA;
- l'APOTEMA di tale poligono tende a coincidere con il RAGGIO.
Ora noi sappiamo che l'AREA di un POLIGONO REGOLARE si calcola nel modo seguente:
A = (P x a)/ 2
dove
A = Area del poligono regolare
P = Perimetro del poligono
a = apotema del poligono.
In altre parole l'area del poligono regolare è uguale al prodotto tra il perimetro del poligono per l'apotema, il tutto diviso due.
Quindi, considerando il cerchio come un poligono inscritto in esso e avente un numero elevatissimo di lati, possiamo dire che la sua area è data dal prodotto tra la lunghezza della circonferenza per il raggio, il tutto diviso due.
In altre parole l'AREA del CERCHIO è uguale a:
A = (C x r)/ 2
dove
A = Area del cerchio
C = Circonferenza
r = raggio.
Noi però sappiamo che la lunghezza della circonferenza si calcola nel modo seguente:
C = 2π x r.
Sostituendo questa formula in quella dell'area otteniamo
A = (2π x r x r)/ 2.
Se in questa formula semplifichiamo il 2 a numeratore e a denominatore e moltiplichiamo, a numeratore, r per r, avremo:
A = π x r2.
Possiamo allora affermare che l'AREA del CERCHIO è data dal PRODOTTO tra il QUADRATO DEL RAGGIO per 3,14.
Da questa formula otteniamo anche la formula inversa che ci permette di calcolare il RAGGIO conoscendo l'area del cerchio, cioè
r2 = A/ π
ovvero
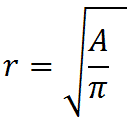
Nella prossima lezione vedremo alcuni esempi di applicazione delle formule appena viste.






