I POLIGONI
In questa lezione e nelle prossime ci occuperemo delle FIGURE GEOMETRICHE PIANE.
Con questa espressione si intende UN QUALSIASI INSIEME DI PUNTI APPARTENENTI AD UNO STESSO PIANO.
Disegniamo il PIANO α:
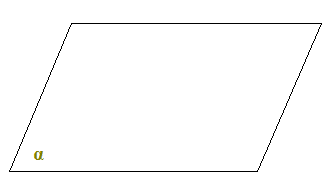
Ricordiamo
α
è una lettera dell'alfabeto greco
e si legge
Alfa.
Ricordiamo pure che il PIANO deve essere immaginato come ESTESO IN TUTTI I SENSI ALL'INFINITO anche se, per poterlo rappresentare, ci limitiamo a disegnare solamente una parte di esso.
Ora disegniamo, sul piano α, una LINEA SPEZZATA SEMPLICE CHIUSA:
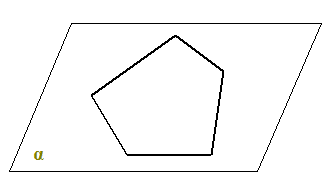
Essa divide il piano in due parti:
- una PARTE ESTERNA che, nel disegno successivo, abbiamo indicato con il colore ARANCIO;
- una PARTE INTERNA che, nel disegno successivo, abbiamo indicato con il colore AZZURRO.

La PARTE ESTERNA è INFINITA o ILLIMITATA, essendo il piano infinito.
La PARTE INTERNA è FINITA o LIMITATA.
La PARTE INTERNA prende il nome di POLIGONO.
Quindi, possiamo dire che un POLIGONO è la PARTE DI PIANO LIMITATA da UNA SPEZZATA SEMPLICE CHIUSA.
D'ora in poi, nel disegnare i poligoni, ometteremo di disegnare il piano.






