FORMULA DI SDOPPIAMENTO NELL'IPERBOLE
- L'iperbole
- Equazione dell'iperbole
- Posizione di una retta rispetto all'iperbole
- Retta tangente all'iperbole e passante per un punto
- Equazione della retta
- Somma di due monomi per la loro differenza
- Fascio di rette passanti per un punto
Nella lezione precedente abbiamo visto come è possibile scrivere l'EQUAZIONE della RETTA TANGENTE ALL'IPERBOLE.
Per risolvere il problema è possibile anche usare un altro metodo che consiste nell'applicare la cosiddetta FORMULA DI SDOPPIAMENTO.
Per vedere di cosa si tratta partiamo dall'EQUAZIONE DELL'IPERBOLE in forma canonica:
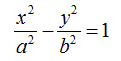
Ora moltiplichiamo entrambi i membri per a2b2 e otteniamo:

da cui abbiamo:
b2x2 - a2y2 = a2b2.
Immaginiamo che le coordinate del punto P siano
P (x0 ; y0).
Nel punto P l'equazione dell'iperbole diventa:
b2x02 - a2y02 = a2b2.
Ora sottraiamo, membro a membro, dall'equazione generale dell'iperbole, l'equazione appena scritta:
b2x2 - a2y2 = a2b2 -
b2x02 - a2y02 = a2b2.
Otterremo:
(x2 - x02)· b2 - (y2 - y02)· a2 = 0
Ora osserviamo che
(x2 - x02)· b2 - (y2 - y02)· a2 = 0
x2 - x02
e
y2 - y02
sono entrambi il PRODOTTO della SOMMA di due MONOMI per la loro DIFFERENZA.
Quindi possiamo scrivere
x2 - x02 = (x- x0) · (x + x0)
e
y2 - y02 = (y- y0) · (y + y0).
Sostituendo avremo:
(x2 - x02)· b2 - (y2 - y02)· a2 = 0
(x - x0) · (x+ x0) · b2 - (y - y0) · (y + y0) · a2 = 0.
Il fascio di rette passante per il punto P ha equazione:
y - y0 = m (x - x0).
Ora sostituiamo a
(y - y0)
il corrispondente
m (x - x0)
e avremo:
(x - x0) · (x + x0) · b2 - m (x - x0) · (y+ y0) · a2 = 0.
A questo punto dividiamo tutto per
(x - x0)
ed otteniamo
(x + x0) · b2 - m · (y+ y0) · a2 = 0.
La nostra equazione, nel punto P assume i seguenti valori:
(x0 + x0) · b2 - m · (y0+ y0) · a2 = 0
da cui otteniamo:
2x0b2 - m2y0a2 = 0.
Ricaviamo il valore di m:
- m2y0a2 = - 2x0b2
m2y0a2 = 2x0b2
m = 2x0b2/ 2y0a2
m = x0b2/ y0a2.
Ora sostituiamo il coefficiente angolare appena trovato nell'equazione del fascio di rette passante per P. Avremo:
y - y0 = m (x - x0)

Moltiplichiamo, primo e secondo membro, per y0a2.
Avremo:
y0a2 · (y - y0) = x0b2 (x - x0).
Eseguiamo i calcoli:
y0a2y - a2y02 = x0b2x - x02b2.
Portiamo tutto a primo membro cambiando di segno:
y0a2y - a2y02 - x0b2x + x02b2 = 0.
Ora noi sappiamo che nel punto P l'equazione dell'iperbole è:
b2x02 - a2y02 = a2b2.
Andiamo allora a sostituire
b2x02 - a2y02
con
a2b2.
Quindi avremo:
y0a2y - a2y02 - x0b2x + x02b2 = 0
y0a2y + x0b2x + a2b2= 0.
Portiamo a secondo membro + a2b2 cambiando di segno:
y0a2y - x0b2x = - a2b2.
Dividiamo entrambi i membri per -a2b2 e avremo:

Cambiamo l'ordine e scriviamo:

La formula appena trovata prende il nome di FORMULA DI SDOPPIAMENTO NELL'IPERBOLE e ci permette di trovare l'equazione della retta tangente all'iperbole e passante per il punto P.
Chiaramente questa formula è valida se ci troviamo di fronte ad un'iperbole con fuochi sull'asse delle ascisse.
Nel caso, invece, in cui l'iperbole ha i fuochi sull'asse delle ordinate la formula di sdoppiamento da usare sarà:

Ovviamente a tale formula si giungerà seguendo lo stesso procedimento con la sola differenza che si dovrà partire dall'equazione canonica dell'iperbole con fuochi sull'asse delle ordinate.
Riprendiamo l'esempio visto nella lezione precedente e vediamo come è possibile risolverlo usando le formule di sdoppiamento.
Esempio:
scrivere l'equazione della retta tangente all'iperbole di equazione

nel punto
P (5; -3).
Applichiamo la formula di sdoppiamento:

Sostituiamo, ai valori di x0 e y0, le coordinate del punto P:

Noi sappiamo anche che
a2 = 16
b2 = 16.
Quindi possiamo scrivere:

Eseguiamo i calcoli:

Abbiamo trovato l'equazione della retta tangente l'iperbole nel punto P e, come possiamo notare, il risultato è lo stesso che avevamo visto nella lezione precedente, ma i conteggi sono molto più semplici.






