DIFFERENZA SIMMETRICA
- Nozione di insieme
- Rappresentazione grafica di un insieme
- Differenza di due insiemi
- Differenza di un insieme con l'insieme vuoto
- Differenza di un insieme con se stesso
- Proprietà della differenza di due insiemi
- Unione di due insiemi
- Intersezione di due insiemi
In una precedente lezione abbiamo parlato della DIFFERENZA tra due INSIEMI.
Dati due insiemi A e B, si chiama DIFFERENZA di A e B, in questo ordine, l'insieme C degli ELEMENTI che APPARTENGONO ad A e che NON APPARTENGONO a B.
In simboli scriveremo:
oppure
che si legge
C uguale A meno B.
Quella che abbiamo appena definito viene detta, a volte, anche DIFFERENZA SEMPLICE per distinguerla dalla DIFFERENZA SIMMETRICA.
Dati due insiemi A e B, si chiama DIFFERENZA SIMMETRICA tra A e B l'insieme C degli ELEMENTI che APPARTENGONO ad A OPPURE APPARTENGONO a B, ma NON APPARTENGONO AD ENTRAMBI.
In simboli scriveremo:
che si legge
C uguale differenza simmetrica tra A e B.
Vediamo come possiamo l'illustrare graficamente la DIFFERENZA SIMMETRICA tramite i DIAGRAMMI DI VENN.
La DIFFERENZA SIMMETRICA tra A e B è l'insieme degli ELEMENTI che APPARTENGONO ad A OPPURE APPARTENGONO a B, ma NON APPARTENGONO AD ENTRAMBI.
Con il colore azzurro abbiamo indicato gli elementi che appartengono ad A, ma non appartengono a B.
Con il colore arancio abbiamo indicato gli elementi che appartengono a B, ma non appartengono ad A.
L'insieme che esprime la DIFFERENZA SIMMETRICA tra A e B l'abbiamo riportata nel diagramma di Venn qui sotto con il colore giallo.
Esistono vari modi per esprimere in simboli l'operazione di DIFFERENZA SIMMETRICA:
che si legge
La differenza simmetrica tra A e B è uguale all'insieme delle x tali che x appartiene ad A e non appartiene a B o x appartiene a B e non appartiene ad A.
Notiamo che le x che appartengono ad A, ma non appartengono a B sono quelle che formano l'insieme
A - B.
Mentre le x che appartengono a B, ma non appartengono ad A sono quelle che formano l'insieme
B - A.
L'insieme degli elementi che appartengono a
(A - B) oppure a (B - A)
non sono altro che
Quindi un altro modo per indicare la DIFFERENZA SIMMETRICA tra A e B è:
che si legge
La differenza simmetrica tra A e B è uguale alla differenza tra A e B unita con la differenza tra B e A.
Vediamo graficamente la situazione:
Un ulteriore modo per esprime la DIFFERENZA SIMMETRICA tra A e B è il seguente:
che si legge
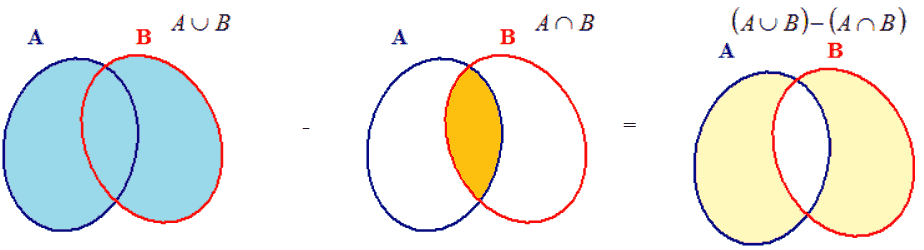
La differenza simmetrica tra A e B è uguale alla differenza tra l'unione di A con B e l'intersezione di A con B.
In quest'ultimo caso noi andiamo a prendere gli elementi che appartengono ad A e gli elementi che appartengono a B (unione di A con B). All'insieme così ottenuto sottraiamo l'insieme degli elementi comuni sia ad A che a B (intersezione di A con B).
Vediamo graficamente la situazione:
Vediamo qualche esempio di DIFFERENZA SIMMETRICA di insiemi.
Esempio:
A = {1, 2, 5, 6, 8 ,10}
B = {2, 6, 7, 9}
A = {a, l, b, e, r, o}
B = {a, r, t, o}
In un prossimo approfondimento vedremo le proprietà della differenza simmetrica.






