FUNZIONI MONOTONE
- Funzioni reali di variabile reale
- Campo di esistenza delle funzioni
- L'insieme dei numeri reali
- Implicazione logica
Sia la FUNZIONE:
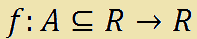
che si legge
f di A, contenuto o uguale ad R, in R.
La funzione si dice MONOTÒNA su A se essa è una:
- FUNZIONE CRESCENTE;
- FUNZIONE NON DECRESCENTE;
- FUNZIONE DECRESCENTE;
- FUNZIONE NON CRESCENTE.
1 - FUNZIONE CRESCENTE
Una funzione è CRESCENTE se dati due valori x1 e x2 appartenenti al suo CAMPO DI ESISTENZA avremo che:
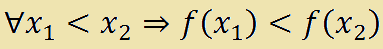
che si legge
qualunque x con 1 minore di x con 2 implica che f con x con 1 è minore di f con x con 2.
Esempio:
y = 2x.
Il campo di esistenza della funzione è dato da ogni x appartenente ai reali.
Disegniamo la nostra funzione:
| x | y |
|---|---|
| -2 | +1/4 |
| -1 | +1/2 |
| 0 | 1 |
| 1 | 2 |
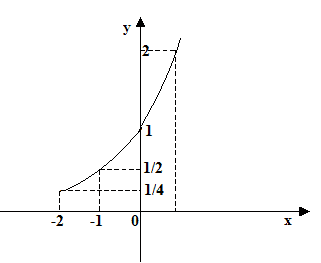
La funzione che abbiamo disegnato è una FUNZIONE CRESCENTE.
2 - FUNZIONE NON DECRESCENTE
Una funzione è NON DECRESCENTE sedati due valori x1 e x2 appartenenti al suo CAMPO DI ESISTENZA avremo che:
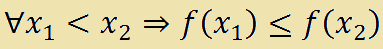
che si legge
qualunque x con 1 minore di x con 2 implica che f con x con 1 è minore o uguale di f con x con 2.
Questo tipo di funzione si dice FUNZIONE NON DECRESCENTE.
Esempio:
Osserviamo ora la seguente funzione:
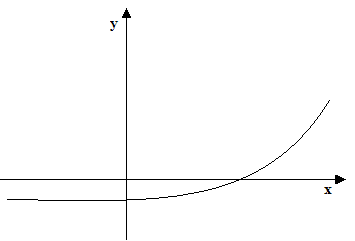
La funzione che abbiamo disegnato è una FUNZIONE NON DECRESCENTE. Infatti, al crescere del valore di x la y in alcuni casi rimane costante, in altri cresce.
3 - FUNZIONE DECRESCENTE
Una funzione è DECRESCENTE se dati due valori x1 e x2 appartenenti al suo CAMPO DI ESISTENZA avremo che:
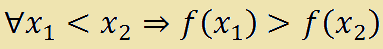
che si legge
qualunque x con 1 minore di x con 2 implica che f con x con 1 è maggiore di f con x con 2.
Questo tipo di funzione si dice FUNZIONE DECRESCENTE.
Esempio:
y = (1/2)x.
Il campo di esistenza della funzione è dato da ogni x appartenente ai reali.
Disegniamo la nostra funzione:
| x | y |
|---|---|
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
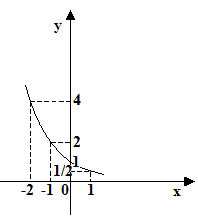
La funzione che abbiamo disegnato è una FUNZIONE DECRESCENTE.
4 - FUNZIONE NON CRESCENTE
Una funzione è NON CRESCENTE se dati due valori x1 e x2 appartenenti al suo CAMPO DI ESISTENZA avremo che:
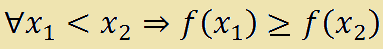
che si legge
qualunque x con 1 minore di x con 2 implica che f con x con 1 è maggiore o uguale a f con x con 2.
Esempio:
Osserviamo ora la seguente funzione:
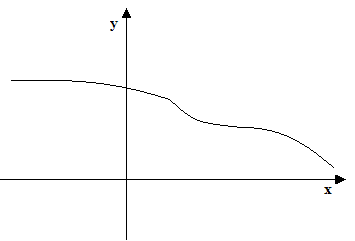
La funzione che abbiamo disegnato è una FUNZIONE NON CRESCENTE. Infatti, al crescere del valore di x la y in alcuni casi rimane costante, in altri decresce.
Le FUNZIONI CRESCENTI e le FUNZIONI DECRESCENTI si dicono MONOTÒNE in SENSO STRETTO.






