FORMULA DI SDOPPIAMENTO NELL'ELLISSE
- L'ellisse
- Posizione di una retta rispetto all'ellisse
- Retta tangente all'ellisse da un punto
- Equazione della retta
- Fascio di rette passanti per un punto
- Somma di due monomi per la loro differenza
Nella lezione precedente abbiamo visto come è possibile scrivere l'EQUAZIONE della RETTA TANGENTE ALL'ELLISSE e passante per un PUNTO sia che esso sia ESTERNO all'ellisse, sia che esso APPARTENGA all'ellisse.
Va detto però che, quando il PUNTO per il quale passa la retta tangente APPARTIENE all'ELLISSE, è possibile usare anche un altro metodo che consiste nell'applicare la cosiddetta FORMULA DI SDOPPIAMENTO.
Ricordiamo che l'EQUAZIONE DELL'ELLISSE è
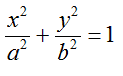
Ora moltiplichiamo entrambi i membri per a2b2 e otteniamo:
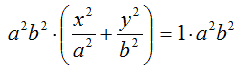
da cui:
b2x2 + a2y2 = a2b2.
Il punto P APPARTENENTE all'ellisse è
P (x0; y0).
Nel punto P l'equazione dell'ellisse diventa:
b2x02 + a2y02 = a2b2.
Ora sottraiamo, membro a membro, dall'equazione generale dell'ellisse, l'equazione appena scritta:
b2x2 + a2y2 = a2b2
b2x02 + a2y02 = a2b2.
Otterremo:
(x2 - x02)· b2 + (y2 - y02)· a2 = 0
Ora osserviamo che
(x2 - x02)· b2 + (y2 - y02)· a2 = 0
x2 - x02
e
y2 - y02
sono entrambi il PRODOTTO della SOMMA di due MONOMI per la loro DIFFERENZA.
Quindi possiamo scrivere
x2 - x02 = (x - x0) · (x + x0)
e
y2 - y02 = (y - y0) · (y + y0).
Sostituendo avremo:
(x2 - x02)· b2 + (y2 - y02)· a2 = 0
(x - x0) · (x + x0) · b2 + (y - y0) · (y + y0)· a2 = 0.
Il fascio di rette passante per il punto P ha equazione:
y - y0 = m (x - x0).
Ora sostituiamo a
(y - y0)
il corrispondente
m (x - x0)
e avremo:
(x - x0) · (x + x0) · b2 + m (x - x0) · (y + y0) · a2 = 0.
A questo punto dividiamo tutto per
(x - x0)
ed otteniamo
(x + x0) · b2 + m · (y + y0) · a2 = 0.
La nostra equazione, nel punto P assume i seguenti valori:
(x0+ x0) · b2 + m · (y0 + y0) · a2 = 0
da cui otteniamo:
2x0b2 + m2y0a2 = 0.
Ricaviamo il valore di m:
m2y0a2 = - 2x0b2
m = - 2x0b2/ 2y0a2
m = -x0b2/ y0a2.
Ora sostituiamo il coefficiente angolare appena trovato nell'equazione del fascio di rette passante per P. Avremo:
y - y0 = m (x - x0)
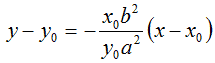
Moltiplichiamo, primo e secondo membro, per y0a2. Avremo:
y0a2 · (y - y0) = -x0b2 (x - x0).
Eseguiamo i calcoli:
y0a2y - a2y02 = -x0b2x + x02b2.
Portiamo tutto a primo membro cambiando di segno:
y0a2y - a2y02 + x0b2x - x02b2 = 0.
Ora noi sappiamo che nel punto P l'equazione dell'ellisse è:
b2x02 + a2y02 = a2b2.
Da cui
- b2x02 - a2y02 = - a2b2.
Andiamo allora a sostituire
- b2x02 - a2y02
con
- a2b2.
Quindi avremo:
y0a2y - a2y02 + x0b2x - x02b2 = 0
y0a2y + x0b2x - a2b2 = 0.
Portiamo a secondo membro - a2b2 cambiando di segno:
y0a2y + x0b2x= a2b2.
Dividiamo entrambi i membri per a2b2 e avremo:
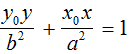
Cambiamo l'ordine e scriviamo:
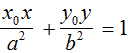
La formula appena trovata prende il nome di FORMULA DI SDOPPIAMENTO NELL'ELLISSE e ci permette di trovare l'equazione della retta tangente all'ellisse e passante per il punto P. Affinché tale formula possa essere applicata è fondamentale che P appartenga all'ellisse. La formula, quindi non è valida se P è un punto esterno all'ellisse.
Riprendiamo l'esempio visto nella lezione precedente e ipotizziamo che sia noto che il punto P appartiene all'ellisse. Vediamo come è possibile risolverlo usando le formule di sdoppiamento.
Esempio:
scrivere l'equazione della retta tangente all'ellisse di equazione
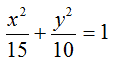
nel punto
P (3; 2).
Sappiamo che P è il punto di tangenza, quindi esso appartiene all'ellisse. Di conseguenza possiamo impiegare le formule di sdoppiamento per risolvere il problema.
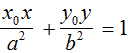
Sostituiamo, ai valori di x0 e y0, le coordinate del punto P:
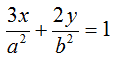
Inoltre sappiamo che
a2 = 15
b2 = 10.
Di conseguenza possiamo scrivere:
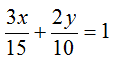
Risolvendo avremo:
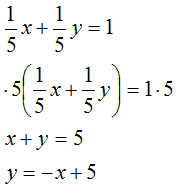
Questa è l'equazione della retta tangente l'ellisse nel punto P.
Come possiamo notare abbiamo ottenuto lo stesso risultato visto nella lezione precedente.






