EQUAZIONE DELL'ELLISSE CON CENTRO NELL'ORIGINE E FUOCHI SULL'ASSE DELLE X
- L'ellisse
- Elementi dell'ellisse
- Il punto
- Distanza tra due punti sul piano
- Elevamento a potenza
- Raccoglimento a fattor comune
- L'insieme dei numeri reali
- Simboli usati per l'insieme dei numeri reali
- Caratteristiche dei triangoli
Nella lezione precedente abbiamo disegnato un'ELLISSE il cui CENTRO è l'ORIGINE DEGLI ASSI e i cui FUOCHI si trovano sull'ASSE delle x:
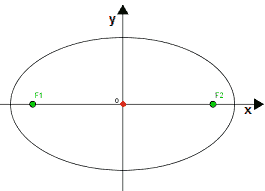
Ora vogliamo cercare di capire qual è l'EQUAZIONE di questa ellisse.
Sappiamo che l'ELLISSE è il luogo geometrico dei PUNTI del piano tali che la SOMMA delle DISTANZE da DUE PUNTI FISSI, detti FUOCHI, è COSTANTE.
Chiamiamo i due FUOCHI, F1 e F2, tali che:
F1 (-c; 0);
F2 (c; 0).
Ora prendiamo un qualsiasi punto P sull'ellisse di coordinate x e y, ovvero:
P (x; y).
Dalla definizione data si deduce che affinché P appartenga all'ellisse deve essere:
PF1 + PF2 = costante.
Ora indichiamo la nostra COSTANTE con 2a. Avremo:
PF1 + PF2 = 2a.
Noi sappiamo che, dati due punti
A (x1; y1)
e
B(x2; y2)
la loro distanza è uguale a:
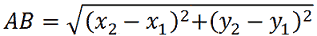
Quindi la distanza PF1 è data da:
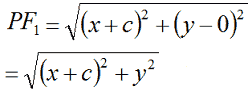
mentre la distanza PF2 è data da:

Quindi
PF1 + PF2 = 2a
può essere scritta come segue:
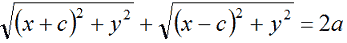
Portiamo a secondo membro il secondo radicale cambiandogli il segno:
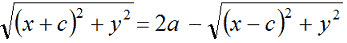
Eleviamo al quadrato primo e secondo membro
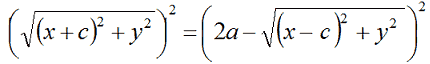
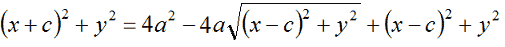
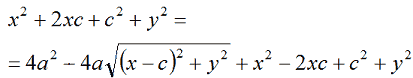
Semplificando avremo:
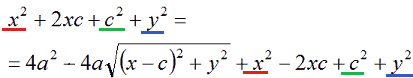
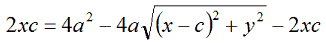
Isoliamo il radicale portandolo a primo membro:
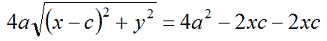
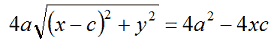
A secondo membro mettiamo in evidenza il 4:
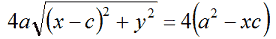
Dividiamo entrambi i membri per 4 e avremo:
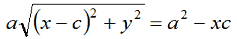
Ora eleviamo al quadrato primo e secondo membro e avremo:
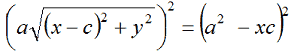
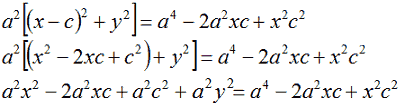
Semplifichiamo:
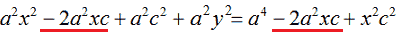
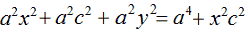
Portiamo a primo membro, cambiando di segno, x2c2, mentre portiamo a secondo membro, sempre cambiando di segno, a2c2:
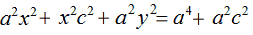
Ora mettiamo in evidenza, a primo membro x2, e a secondo membro a2. Avremo:
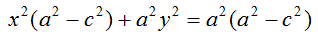
Ora poniamo
a2 - c2 = b2.
Tale sostituzione è possibile perché esiste sempre un valore di b appartenente all'insieme dei reali positivi R+ tali che
a2 - c2 = b2 .
Vediamone il perché.
Disegniamo il punto P appartenente all'ellisse e i fuochi F1 e F2:
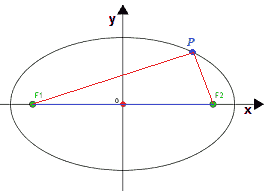
I segmenti PF1, PF2, F1F2 sono i lati di un TRIANGOLO.
Indichiamo la lunghezza del segmento F1F2 con 2c, ovvero
F1F2 = 2c.
Ora, noi sappiamo che in un TRIANGOLO OGNI LATO è sempre MINORE della SOMMA DEGLI ALTRI DUE.
Quindi possiamo scrivere:
F1F2 < PF1 +PF2 .
Ma poiché
F1F2 = 2c
e
PF1 +PF2 = 2a
possiamo dire che
2c < 2a
ovvero
c < a
quindi
c2 < a2
da cui
c2 - a2 < 0
ovvero
a2 - c2 > 0.
Quindi ci sarà sempre un valore di b appartenente all'insieme dei reali positivi R+ tale che
a2 - c2 = b2 .
Ora, torniamo alla nostra equazione, ed effettuiamo la sostituzione detta.
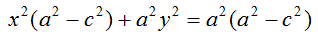
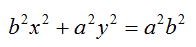
Dividiamo entrambi i membri per a2b2:
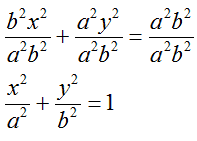
Dunque:
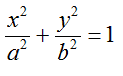
è l'equazione dell'ellisse da noi disegnata.
Come possiamo notare si tratta di un'ELLISSE che ha:
- il CENTRO nell'ORIGINE degli assi;
- i FUOCHI sull'ASSE DELLE x.
Quindi
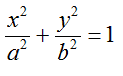
è l'EQUAZIONE DELL'ELLISE con CENTRO nell'ORIGINE degli assi e FUOCHI sull'ASSE delle x.
Concludiamo questa lezione dicendo che, quando l'ellisse ha come ASSI di SIMMETRIA gli ASSI CARTESIANI prende il nome di ELLISSE CANONICA.






