DISEQUAZIONI CON VALORE ASSOLUTO ED UNA COSTANTE
- I numeri relativi
- Valore assoluto: concetti base
- Nozione di valore assoluto
- Disequazioni con valore assoluto
- Disequazioni con valore assoluto e lo zero
- Disequazioni con valore assoluto e una costante
In questa lezione e nella prossima vedremo come si risolvono le disequazioni che si presentano in una delle seguenti forme:
|A(x)| > k
|A(x)| < k
dove k è una costante.
Così come abbiamo detto nella lezione precedente, anche in questo caso:
- anziché il simbolo di maggiore possiamo trovare quello di maggiore o uguale;
- come, anziché il simbolo di minore possiamo trovare quello di minore o uguale.
In questa lezione ci concentreremo sul caso di disequazioni con il simbolo di maggiore o maggiore uguale, quindi disequazioni del tipo
|A(x)| > k
oppure
|A(x)| ≥ k.
Bisogna distinguere il caso in cui k è negativo, da quello in cui kè positivo.
Partiamo da
k < 0.
A primo membro abbiamo un valore assoluto: esso è sempre positivo, quindi la nostra disequazione è sempre vera dato che un valore positivo è sempre maggiore di uno negativo. Anche nel caso in cui la x dovesse assumere dei valori tali che A(x) è uguale a zero, la disequazione è vera dato che lo zero è maggiore di un numero negativo.
In altre parole la soluzione è data da:

che si legge
qualunque x appartenente ai reali.
Esempio:
|6x - 2| > -4.
Nel nostro esempio
k = - 4
quindi un valore negativo. Il primo membro è sempre positivo e, quindi, sempre maggiore del secondo. La disequazione è sempre vera per qualsiasi valore di x.
E se anziché il simbolo di maggiore, nella disequazione vi fosse stato il simbolo di maggiore o uguale? In altre parole vogliamo vedere cosa accade se la disequazione ha una forma del tipo:
|A(x)| ≥ k
sempre con
k < 0.
Ovviamente non cambia nulla dato che dovremmo includere nella soluzione anche i valore di x che annullano A(x) ma abbiamo visto che essi sono già compresi nel caso in cui la disequazione preveda il solo simbolo di maggiore.
Passiamo ad esaminare il caso in cui
|A(x)| > k
con
k > 0.
Per risolvere questo tipo di disequazione ricorriamo alla definizione di valore assoluto ed in modo particolare consideriamo il VALORE ASSOLUTO di un numero o di una espressione come la sua DISTANZA DALL'ORIGINE di una linea dei numeri.
Prendiamo allora il numero reale k: la sua distanza dall'origine è k. Ma anche il numero -k ha una distanza dall'origine pari a k. Graficamente:
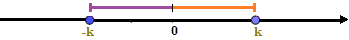
E' evidente che, il segmento 0k è il segmento -k0 sono congruenti cioè, in altre parole, coincidono.
Ora chiediamoci: "Quando il valore assoluto di un'espressione è maggiore di k?". Ciò si verifica quando la distanza dall'origine è maggiore rispetto alla distanza 0k oppure quando la distanza dall'origine è maggiore rispetto alla distanza -k0.
Ad esempio quando

In altre parole, questo si verifica ogni volta che la nostra espressione si colloca nell'area tratteggiata del grafico:

cioè ogni volta in cui A(x) è maggiore di k oppure A(x) è minore di -k.
In altre parole le soluzioni della disequazione sono
A(x) > k ˅ A(x) < - k
che si legge
A con x maggiore di k oppure A con x minore di meno k.
Esempio:
|5x + 2| > 12.
Il verso della disequazione è maggiore e k è un numero positivo, 12: si tratta, quindi, di risolvere
5x + 2 > 12 ˅ 5x + 2 < - 12.
Risolviamo la prima disequazione:
5x + 2 > 12
5x > 12 - 2
5x > 10
x > 5/10
x > 2.
Passiamo alla seconda disequazione
5x + 2 < - 12
5x < -12 - 2
5x < -14
x < -14/5.
La nostra disequazione di partenza ha, quindi, come soluzioni
x > 2 ˅ x < -14/5.
E se la nostra disequazione presentasse, oltre al simbolo di maggiore, anche quello di uguale? Non cambia nulla. Basta aggiungere il simbolo di uguale anche nel risultato, cioè includere nel risultato anche i valori di x che rendono nullo A(x).
Quindi, se
A(x) ≥ k
con
k > 0
le soluzioni saranno
A(x) ≥ k ˅ A(x) ≤ - k.
Esempio:
|3x - 6| 18
3x - 6 ≥ 18 ˅ 3x - 6 ≤ - 18.
Risolviamo la prima disequazione:
3x - 6 ≥ 18
3x ≥ 18 + 6
3x ≥ 24
x ≥ 24/3
x ≥ 8.
Passiamo alla seconda disequazione:
3x - 6 ≤ - 18
3x ≤ - 18 + 6
3x ≤ - 12
x ≤ -12/3
x ≤ -4
La nostra disequazione di partenza ha, quindi, come soluzioni
x ≥ 8 ˅ x ≤ -4.
Nella prossima lezione vedremo cosa accade nelle disequazioni con valore assoluto e una costante e il simbolo di minore.
Inoltre, quello che abbiamo visto in questa lezione non è il solo modo per risolvere una disequazione di questo tipo: se volte saperne di più leggete l'approfondimento Risoluzione di disequazioni con valore assoluto e costante: vi suggeriamo, però, di leggerlo dopo aver letto la prossima lezione.






