OMOTETIA DIRETTA
Abbiamo accennato, nella lezione precedente, al concetto di TRASFORMAZIONI NON ISOMETRICHE.
In questa lezione ci occuperemo della OMOTETIA. Essa può essere:
- DIRETTA;
- INVERSA.
In questa lezione parleremo della OMOTETIA DIRETTA, mentre quella indiretta verrà esamianta nelle prossime lezioni.
Disegniamo su un piano α (che si legge alfa) due punti: il punto O e il punto P.
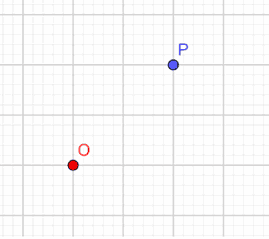
Ora fissiamo un numero reale k, tale che esso sia POSITIVO e DIVERSO DA ZERO. In altre parole esso dovrà essere
k > 0.
Ad esempio poniamo
k = 2.
Ora disegniamo la retta r passante per i punti O e P.
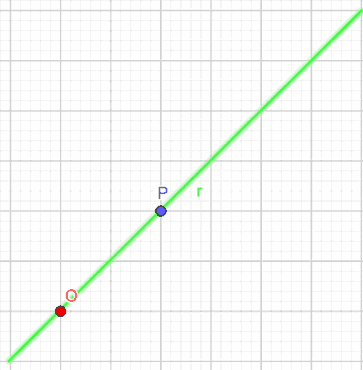
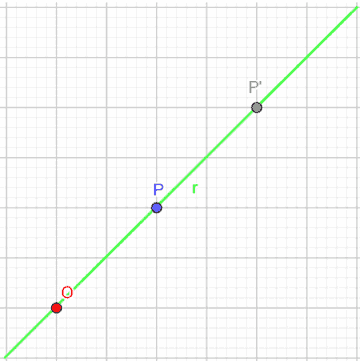
Determiniamo la distanza
OP e stacchiamo sulla retta
r, dalla STESSA PARTE del punto P,
il punto
P' in modo tale che
la distanza OP' sia uguale a
k volte OP.
Nel nostro caso, avendo posto
k = 2
OP' dovrà essere 2 volte OP, ovvero
OP' = 2 · OP.
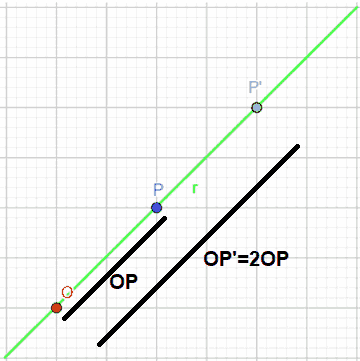
Quella che abbiamo appena visto è una OMOTETIA DIRETTA.
Ora osserviamo che, essendo
OP' = 2 · OP
possiamo dividere entrambi i membri per OP ed ottenere
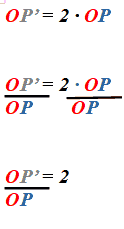
Quindi, per OMOTETIA DIRETTA si intende una TRASFORMAZIONE che, dato un punto O ed un NUMERO REALE k, POSITIVO e DIVERSO da ZERO, associa ad ogni punto P del piano, il punto P' allineato con O e con P, tali che P e P' siano situati dalla STESSA PARTE rispetto ad O e tali che il rapporto tra OP' ed OP sia UGUALE a k.
Il punto O è detto CENTRO della OMOTETIA, mentre k è detto RAPPORTO della omotetia o anche CARATTERISTICA.
Una OMOTETIA di CENTRO O e rapporto k si indica con il simbolo
ωo,k
che si legge
omotetia di centro O e rapporto k
Nella prossima lezione vedremo come costruire l'omotetia diretta di una figura piana.






