RADICE DI UN RADICALE
- Radicali di indice n
- Radicali con indice dispari
- Condizione di esistenza dei radicali
- Potenze con esponente frazionario
- Proprietà delle potenze
- L'insieme dei numeri naturali
- Simboli usati per l'insieme dei numeri naturali
- L'insieme dei numeri reali
In questa lezione vogliamo vedere come è possibile calcolare la RADICE di un RADICALE.
La RADICE di un RADICALE è una RADICE che ha:
- per indice il PRODOTTO degli indici;
- per radicando lo stesso radicando.
In altre parole:
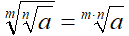
Bisogna tenere presente che:
- se
m O
n sono PARI
allora è necessario che
a ≥ 0;
- se m ED n sono DISPARI allora a può essere anche negativo.
Quindi possiamo dire che:
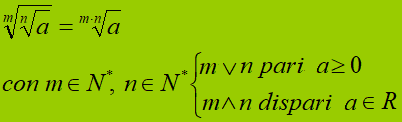
che si legge
la radice emmesima della radice ennesima di a
è uguale
alla radice di indice m per n
con
m ed n appartenenti ad enne asterisco (ovvero l'insieme dei numeri naturali escluso lo zero) e
se
m o n è pari, a maggiore o uguale a zero
se m e n sono dispari a appartenente ai reali.
Dimostriamo quanto abbiamo detto. Dallo studio delle potenze con esponente frazionario sappiamo che:
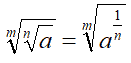
Proseguendo allo stesso modo si può scrivere:
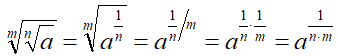
Da cui si ottiene:
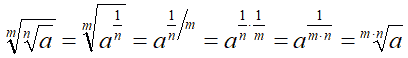
Abbiamo quindi dimostrato che:
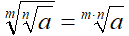
Ovviamente la regola può essere estesa anche al caso di più radici. Esempio:
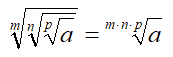
Vediamo alcuni esempi:
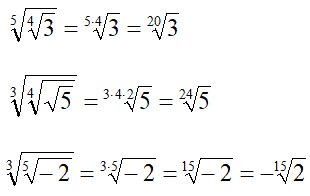
In questo ultimo caso entrambi gli indici dei radicali sono dispari, quindi possiamo procedere anche se il radicando è negativo. Ricordiamo, inoltre, che nel caso di radicali con indice dispari e con radicando negativo è possibile portare il segno meno fuori dalla radice senza che il risultato cambi.






