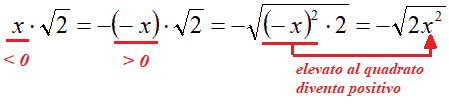TRASPORTO DI UN FATTORE DENTRO IL SEGNO DI RADICE
- Radicali di indice n
- Radicali con indice dispari
- Trasporto di un fattore fuori dal simbolo della radice
- Trasporto di un fattore fuori dal simbolo della radice
- Trasporto di un fattore fuori dal simbolo della radice
- Trasporto di un fattore fuori dal simbolo della radice
- L'insieme dei numeri naturali
- Simboli usati per l'insieme dei numeri naturali
- L'insieme dei numeri reali
Dopo aver parlato del TRASPORTO di un fattore FUORI del simbolo di RADICE, ora vedremo come procedere nel caso in cui vogliamo portare un FATTORE DENTRO il segno di RADICE.
In pratica stiamo esaminando l'operazione inversa rispetto a quella vista nelle lezioni precedenti.
Quindi, se noi abbiamo
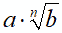
vogliamo portare la a sotto il segno di radice.
Ora, parlando del trasporto di un fattore fuori dal segno di radice, abbiamo detto che
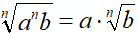
Per la proprietà transitiva dell'uguaglianza possiamo dire che:
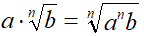
Quindi, per PORTARE DENTRO la RADICE un fattore esterno, è sufficiente ELEVARLO alla potenza di esponente UGUALE all'INDICE del radicale.
Per tanto possiamo scrivere:
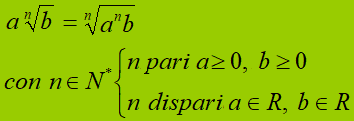
che si legge
a per radice ennesima di b
è uguale
alla radice ennesima di a elevato ad n per b
con
n appartenente ad enne asterisco (ovvero l'insieme dei numeri naturali escluso lo zero) e
se n è pari, a maggiore o uguale a zero e b maggiore o uguale a zero
se n è dispari a appartenente ai reali e b appartenente ai reali.
Vediamo alcuni esempi:
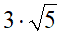
In questo caso l'indice del radicale è pari, inoltre 3 e 5 sono numeri positivi quindi possiamo limitarci ad applicare la formula. Avremo:
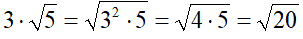
Secondo esempio:
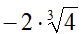
In questo caso l'indice del radicale è dispari, quindi possiamo passare ad applicare la formula. Possiamo procedere in due modi diversi:
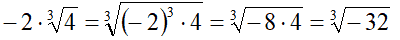
oppure
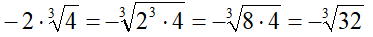
Ricordiamo, infatti, che nel caso di radicali con indice dispari e con radicando negativo è possibile portare il segno meno fuori dalla radice senza cambiarne il risultato.
Altro esempio:
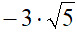
In questo caso abbiamo un numero negativo davanti ad un radicale di indice pari.
Poiché sotto la radice dobbiamo avere due numeri positivi, lasciamo il segno negativo fuori dalla radice e portiamo sotto la radice il valore assoluto del numero. Così:
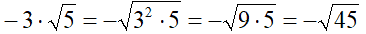
Infine vediamo un ultimo esempio
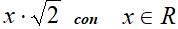
Ora osserviamo che, portando x sotto la radice, diventa x2 che è sempre un numero positivo. Quindi possiamo portarlo senza problemi sotto il simbolo della radice.
Però, dato che non sappiamo se x è positivo o negativo, dobbiamo distinguere i due casi. Quindi, avremo:
- se x
≥ 0
avremo
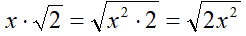
- se x
< 0
avremo