ELEMENTI DI SIMMETRIA DEI PARALLELOGRAMMI
- Parallelogramma
- Rettangolo
- Rombo
- Quadrato
- Trapezio isoscele
- Figure geometriche equivalenti e figure geometriche congruenti
Disegniamo il PARALLELOGRAMMA ABCD e le sue DIAGONALI:
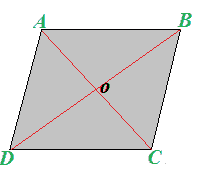
Il punto O in cui le diagonali si INTERSECANO rappresenta il CENTRO DI SIMMETRIA del parallelogramma.
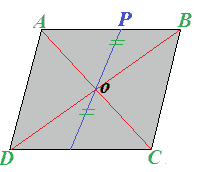
Se segniamo un qualsiasi punto P su uno dei suoi lati, lo congiungiamo con il punto O e prolunghiamo il segmento PO, vedremo che esso interseca il lato opposto nel punto P'.
Con un righello possiamo facilmente verificare che il segmento PO e il segmento OP' sono CONGRUENTI.
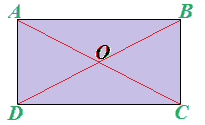
Il RETTANGOLO è un parallelogramma. Quindi, anche il CENTRO DI SIMMETRIA del rettangolo è dato dal PUNTO DI INTERSEZIONE DELLE SUE DIAGONALI:
Se disegniamo i punti medi dei 4 lati (M, M', N e N') e uniamo i punti medi del lati opposti mediante le rette r ed s notiamo che tali rette sono anche gli ASSI DI SIMMETRIA del rettangolo.
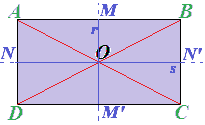
L'ASSE DI SIMMETRIA è una retta che divide la figura in due parti specularmente uguali.
Il ROMBO è un parallelogramma. Quindi, anche il CENTRO DI SIMMETRIA del rombo è dato dal PUNTO DI INTERSEZIONE DELLE SUE DIAGONALI:
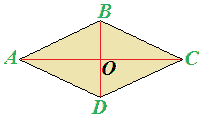
Le DIAGONALI rappresentano anche gli ASSI DI SIMMETRIA.
Il QUADRATO è un parallelogramma. Quindi, anche il CENTRO DI SIMMETRIA del quadrato è dato dal PUNTO DI INTERSEZIONE DELLE SUE DIAGONALI:
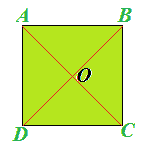
Possiamo notare che le DIAGONALI rappresentano anche gli ASSI DI SIMMETRIA.
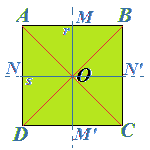
Ma possiamo disegnare altri due ASSI DI SIMMETRIA. Disegniamo i punti medi dei 4 lati (M, M', N e N') e uniamoli a due a due mediante le rette r ed s: notiamo che tali rette sono anch'esse gli ASSI DI SIMMETRIA del quadrato.
Il quadrato, quindi, ha 4 assi di simmetria..
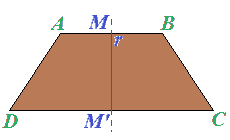
Disegniamo, ora, un TRAPEZIO ISOSCELE.
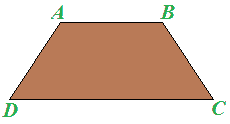
Ora segniamo i punti medi della base maggiore e della base minore: li indichiamo con M e M'. Li uniamo tracciando la retta r.
Tale retta è l'ASSE DI SIMMETRIA del TRAPEZIO ISOSCELE.