POLIGONI REGOLARI CIRCOSCRITTI
- Poligoni equiangoli poligoni equilateri poligoni regolari
- Poligoni inscritti
- Poligoni regolari inscritti
- Poligoni circoscritti
- La circonferenza e il cerchio
- Bisettrice di un angolo
- Incentro
- Circocentro
- Posizioni di una retta rispetto ad una circonferenza
Riprendiamo il poligono inscritto visto nella lezione precedente:
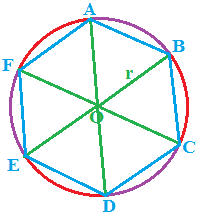
Sempre nella lezione precedente abbiamo dimostrato che tale poligono è un POLIGONO REGOLARE, cioè un poligono equilatero ed equiangolo.
Ora vogliamo disegnare le BISETTRICI relative ai vertici del poligono. Ricordiamo che la bisettrice di un angolo è la semiretta che ha per origine il vertice dell'angolo e che divide l'angolo in due parti uguali.
Nella lezione precedente abbiamo visto che ognuno dei triangoli AOB, BOC, COD, DOE, EOF, FOA ha gli angoli alla base congruenti e che tali triangoli sono tutti congruenti tra loro. Ne consegue che le bisettrici degli angoli dei poligoni sono rispettivamente i segmenti AO, BO, CO, DO, EO, FO.
Il punto in cui si incontrano tali bisettrici è l'INCENTRO, ed è evidente che esso coincide con il CENTRO DELLA CIRCONFERENZA e sappiamo che questa è la condizione affinché un poligono sia circoscrittibile alla circonferenza.
Possiamo allora affermare che se un POLIGONO è REGOLARE esso è SEMPRE CIRCOSCRITTIBILE nella circonferenza. In esso esiste un solo incentro che è anche il centro della circonferenza.
Per disegnare il poligono circoscritto alla circonferenza è sufficiente disegnare le TANGENTI alla circonferenza nei punti di divisione A, B, C, D, E, F:
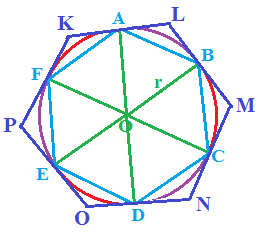
In questo modo abbiamo disegnato il poligono KLMNOP.
Abbiamo così disegnato un POLIGONO REGOLARE CIRCOSCRITTO ALLA CIRCONFERENZA.






