TEOREMA DI PITAGORA E TRAPEZIO RETTANGOLO
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Le formule inverse del teorema di Pitagora
- Trapezio rettangolo
- Rettangolo
- Triangolo rettangolo
- Perimetro di un poligono
Disegniamo il TRAPEZIO RETTANGOLO ABCD:
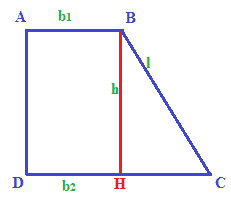
Nell'immagine sopra abbiamo indicato con:
b2
= la base maggiore;
b1
= la base minore;
l
= il lato obliquo;
h
= l'altezza.
Possiamo osservare che l'altezza BH divide il trapezio rettangolo in due figure:
- il rettangolo ABHD;
- il triangolo rettangolo BHC.
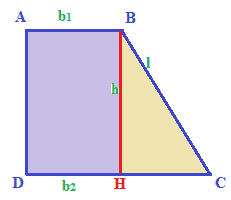
Ora poniamo la nostra attenzione sul triangolo BHC. Esso ha:
- per IPOTENUSA il lato obliquo del trapezio l;
- per CATETI:
- l'altezza del trapezio h;
-
il segmento HC.
Ora osserviamo proprio il segmento HC: esso è dato dalla differenza tra la base maggiore e la base minore, quindi possiamo scriverlo come:
HC = b2 - b1.
Applicando il teorema di Pitagora al TRAPEZIO RETTANGOLO possiamo scrivere le seguenti formule:
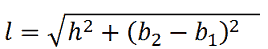
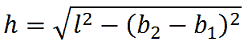
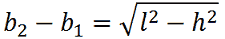
Esempio:
calcolare il perimetro di un trapezio rettangolo che ha la base maggiore di m 24, la base minore di m 18,4 e l'altezza di m 19,2.
Per poter trovare il perimetro del trapezio rettangolo dobbiamo conoscere la misura di tutti i suoi lati. Noi conosciamo la base maggiore e la base minore e conosciamo la misura del lato AD. Ci resta da trovare la misura del lato obliquo.
Applichiamo il teorema di Pitagora e abbiamo:
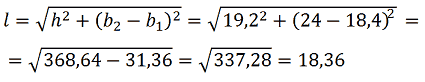
Sappiamo, allora, che il lato misura m 18,36.
Possiamo, quindi, trovare il nostro perimetro:
P = 24 + 18,36 + 18,4 + 19,2 = m 79,96.






