POTENZE DI NUMERI RELATIVI

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• I numeri relativi
• Rappresentazione grafica numeri relativi
• Operazioni con i numeri relativi
• Proprietà delle potenze di numeri relativi
• Potenze di numeri relativi con esponente negativo
• Elevamento a potenza

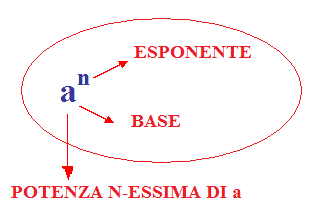
Prendiamo un numero relativo che chiameremo a.

Ora supponiamo che il numero n sia un numero intero positivo (esempio +1, +2, + 3, +4, ecc..).

Chiameremo potenza n-essima (si legge ennesima) di a il prodotto di n fattori uguali ad a.

Questa potenza si rappresenta col simbolo aⁿ.

Esso sta ad indicare che dobbiamo moltiplicare a per se stesso n volte.

Esempio:

(+2)³ = (+2) x (+2) x (+2)

(-5)⁴ = (-5) x (-5) x (-5) x (-5)

(-3)⁵ = (-3) x (-3) x (-3) x (-3) x (-3).

Il numero a prende il nome di base, mentre n si dice esponente o grado della potenza.

Per convenzione si ha che:

a¹ = a

mentre

a⁰ = 1 a condizione che a sia diverso da zero, cioè 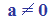. Infatti, se a fosse uguale a zero, avremmo 0⁰ che non ha significato.

Ricapitolando

aⁿ
potenza n-essima di a (si legge potenza ennesima di a)
significa moltiplicare a per se stesso per n volte

a
NUMERO RELATIVO

n
NUMERO INTERO POSITIVO

a
BASE

n
ESPONENTE

a¹ = a

a⁰ = 1

Vediamo ora come si esegue la potenza di un numero relativo, posto che n sia un numero intero positivo (delle potenze di numeri relativi con esponente negativo parleremo in un'altra lezione).

La potenza del numero relativo aⁿ si determina nel modo seguente:

• il suo valore assoluto si ottiene moltiplicando il valore assoluto per se stesso per n volte.
• il suo segno sarà positivo se l'esponente è pari, mentre risulterà invariato rispetto al segno della base se l'esponente è dispari.

Cioè:

aⁿ
valore assoluto: a x a x a ...... (per n volte)
segno: positivo se n è pari
segno: invariato rispetto alla base se n è dispari

Esempio:
(+2)³
valore assoluto del risultato: 2 x 2 x 2 = 8

segno: invariato rispetto alla base essendo n dispari

(+2)³ = +8

Esempio:
(-2)²
valore assoluto del risultato: 2 x 2 = 4
segno: positivo essendo n dispari (-2)² = +4

Esempio:
(-3)³ = valore assoluto del risultato: 3 x 3 x 3 = 27
segno: n = 3; dispari; segno uguale a quello della base, cioè -
(-3)³ = -27

Per approfondire questo argomento, leggi:

• Le proprietà delle potenze di numeri relativi con esponente negativo

Esercizi su questo argomento:

• Esercizio 40 - Potenze di numeri relativi
• Esercizio 41 - Potenze di numeri relativi
• Esercizio 42 - Potenze di numeri relativi

Lezione precedente - Lezione successiva

Indice degli argomenti sui numeri relativi

Pubblicità/Advertising