PROPRIETA' DELLE POTENZE DI NUMERI RELATIVI CON ESPONENTE NEGATIVO
- I numeri relativi
- Potenze di numeri relativi
- Proprietà delle potenze di numeri relativi
- Potenze di numeri relativi con esponente negativo
Una potenza ad esponente negativo è uguale ad una frazione che ha per numeratore l'unità e per denominatore la potenza della stessa base con esponente positivo.
Cioè:
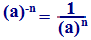
Esempio:
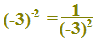
Le potenze con ESPONENTE INTERO NEGATIVO godono di tutte le proprietà delle POTENZE AD ESPONENTE INTERO POSITIVO.
Vediamo la loro dimostrazione.
- Il
prodotto di due o più potenze aventi la stessa base è
una potenza della stessa base con esponente uguale alla
somma degli esponenti.
Quindi
a-m a-n = a (-m)+(-n) = a -m-n
Infatti:
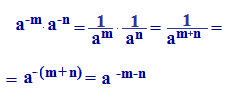
-
Il quoziente di due o più potenze aventi la stessa base è una potenza della stessa base con esponente uguale alla differenza degli esponenti.
Quindi
a-m : a-n = a (-m)-(-n) = a -m+n
Infatti:
- La
potenza di una potenza è una potenza che ha per base la stessa
base e per esponente il prodotto degli esponenti.
Quindi
(a-m)-n = a (-m)(-n)
Infatti:
-
Il prodotto tra due o più potenze aventi gli stessi esponenti è uguale ad una potenza che ha per base il prodotto delle basi e per esponente lo stesso esponente.
Quindi
a-m b-m = (a b)-m
Infatti:
- Il
quoziente tra due potenze aventi gli stessi esponenti
è uguale ad una potenza che ha per base il quoziente delle
basi e per esponente lo stesso esponente.
Quindi
a-m : b-m = (a : b)-m .
Infatti:
- Esercizio 47 - Potenze di numeri relativi con esponente negativo
- Esercizio 48 - Potenze di numeri relativi con esponente negativo
- Esercizio 49 - Potenze di numeri relativi con esponente negativo






