PROPRIETA' DELLA POTENZA DI UNA MATRICE
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- Matrice
- Operazioni tra matrici
- Prodotto tra matrici
- Proprietà del prodotto tra matrici
- Matrice quadrata
- Potenza di matrici quadrate
- Elevamento a potenza
- Quadrato di un binomio
Nella lezione precedente abbiamo visto come è possibile calcolare la POTENZA di una MATRICE QUADRATA.
In questa lezione vedremo di quali PROPRIETA' gode la POTENZA di una MATRICE.
Data una MATRICE QUADRATA A, possiamo dire che:
- An · Am = An+m;
- (An)m = An·m.
Notiamo anche che:
(A + B)2 =
= (A + B) · (A + B).
Per la PROPRIETA' DISTRIBUTIVA DEL PRODOTTO RISPETTO ALLA SOMMA possiamo scrivere che:
(A + B) · (A + B) =
A · (A + B) + B · (A + B) =
A2 + AB + BA + B2.
Poiché il PRODOTTO TRA MATRICI NON gode della PROPRIETA' COMMUTATIVA possiamo dire che:
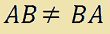
e di conseguenza
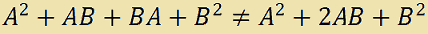
come invece si potrebbe immaginare dallo studio del quadrato di un binomio.
