RELAZIONE D'ORDINE
- Relazioni in un insieme
- Proprietà delle relazioni su un insieme
- Proprietà riflessiva di una relazione in un insieme
- Proprietà simmetrica di una relazione in un insieme
- Proprietà antisimmetrica di una relazione su un insieme
- Proprietà transitiva di una relazione su un insieme
- Implicazione logica
- L'insieme dei numeri naturali
Una relazione 
in un insieme A si
dice RELAZIONE D'ORDINE in A
se gode delle seguenti proprietà:
In questo caso si
dice che l'insieme A
è ORDINATO dalla RELAZIONE
.
Sappiamo che, se a
e b sono legati dalla relazione
,
si scrive
che si legge
a associato b mediante .
Se tra a e b esiste una RELAZIONE D'ORDINE scriveremo:
che si legge
a minore o uguale a b
oppure
a precede o coincide con b.
Si preferisce dire "a è minore o uguale a b" quando a e b sono due NUMERI.
Mentre si è soliti dire "a precede o coincide con b" quando a e b sono due PUNTI su una retta orientata.
Scrivere:
equivale a scrivere
che si legge
b maggiore o uguale ad a
oppure
b segue o coincide con a.
Sappiamo che la PROPRIETA' RIFLESSIVA DI UNA RELAZIONE si può esprimere così:
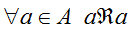
che si legge
per qualunque a appartenente ad A, a associato ad a mediante R.
La PROPRIETA' ANTISIMMETRICA DI UNA RELAZIONE si può esprimere così:
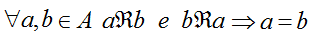
che si legge
se per qualunque a e b appartenenti ad A, a associato a b mediante R e b associato ad a mediante R allora a è uguale a b.
La PROPRIETA' TRANSITIVA DI UNA RELAZIONE si può esprimere così:
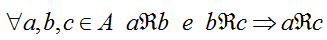
che si legge
se per qualunque a, b, c appartenenti ad A, a associato a b mediante R e b associato a c mediante R allora a è associato a c mediante R.
Quando ci troviamo di fronte ad una RELAZIONE D'ORDINE scriveremo:
| PROPRIETA' | RELAZIONE | RELAZIONE D'ORDINE |
|---|---|---|
| RIFLESSIVA |  |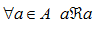
 |
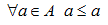| ANTISIMMETRICA |  |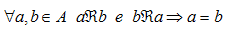
 |
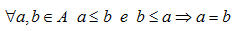| TRANSITIVA |  |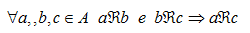
 |
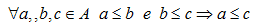Vediamo come
riconoscere se una relazione
su un insieme A è una RELAZIONE
D'ORDINE.
Consideriamo:
A = {abitanti dell'Italia}
= abita nella stessa città di
E' evidente che la relazione è riflessiva.
Essa è anche transitiva perché, posto che a, b e c appartengano all'insieme A, se a abita nella stessa città di b e b abita nella stessa città di c, è evidente che anche a e c abitano nella stessa città.
La relazione però non è anche antisimmetrica, infatti, se a abita nella stessa città di b e b abita nella stessa città di a non significa che a e b siano la stessa persona.
Quindi la relazione " abita nella stessa città di" sull'insieme degli "abitanti dell'Italia" NON è una RELAZIONE D'ORDINE.
Ora consideriamo
N = {numeri naturali}
= è minore o uguale di
E' evidente che la relazione è riflessiva dato che ogni numero è uguale a se stesso.
La relazione è anche antisimmetrica perché, posto che a, b siano due numeri naturali, se a è minore o uguale a b e b è minore o uguale ad a significa che a e b sono uguali.
Essa è anche transitiva, perché se a è minore o uguale a b e b è minore o uguale a c, senz'altro a è minore o uguale a c.
Quindi la relazione "è minore o uguale di" sull'insieme dei "numeri naturali" è una RELAZIONE D'ORDINE.
