FUNZIONI INVERSE
- Funzioni reali di variabile reale
- Nozione di insieme
- Funzioni iniettive
- Come riconoscere se una funzione è iniettiva
- Come capire se una funzione è iniettiva
- Funzioni suriettive
- Come riconoscere se una funzione è suriettiva
- Funzioni biunivoche
- Come riconoscere se una funzione è biunivoca
- Sottoinsiemi propri e impropri
- L'insieme dei numeri reali
Sia f una funzione reale di variabile reale definita su un insieme A tale che associa ad ogni x appartenente all'insieme A uno e un solo y appartenente all'insieme B:
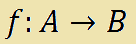
che si legge
f di A in B
Ora vogliamo vedere se è possibile trovare una funzione g che associ ad ogni y appartenente all'insieme B uno e un solo elemento x appartenente all'insieme A. Ovvero vogliamo vedere se esiste
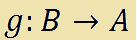
che si legge
g di B in A
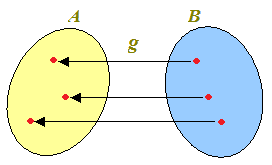
E' evidente che non sempre ciò è possibile, in quanto un elemento di B potrebbe avere in A più di un corrispondente.
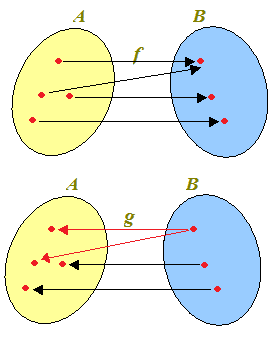
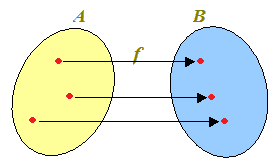
Nell'esempio riportato sopra accade che due elementi di A sono associati, mediante la funzione f, ad un solo elemento di B.
In questo caso non è possibile trovare una funzione g che associ ad ogni elemento di B un solo elemento di A perché, in un caso (lo abbiamo evidenziato con le frecce rosse), ad un elemento di B sono associati due elementi di A.
Quindi possiamo trovare la nostra funzione g solamente se ad ogni elemento x appartenente all'insieme A corrisponde un solo elemento y appartenente all'insieme B. Ma sappiamo che, quando ciò si verifica, la nostra funzione si dice INIETTIVA.
Ma vediamo ancora un'altra ipotesi.
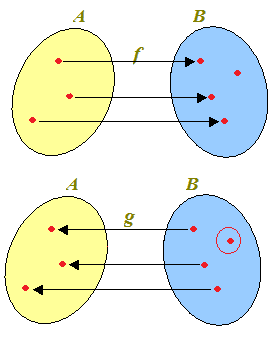
Nell'esempio riportato sopra accade che un elemento di B non è associato, mediante la funzione f, a nessun elemento di A.
In questo caso non è possibile trovare una funzione g che associ ad ogni elemento di B un solo elemento di A perché in un caso (lo abbiamo cerchiato di rosso) un elemento di B non è associato a nessun elemento di A.
Quindi possiamo trovare la nostra funzione g solamente se ogni elemento dell'insieme B è immagine di almeno un elemento dell'insieme A. Ma sappiamo che, quando ciò si verifica, la nostra funzione si dice SURIETTIVA.
Quindi, affinché una funzione sia INVERTIBILE essa deve essere INIETTIVA e SURITTIVA. Ma una funzione che è, al tempo stesso, iniettiva e suriettiva è una FUNZIONE BIUNIVOCA.
Quindi, affinché una funzione sia INVERTIBILE essa deve essere BIUNIVOCA.
A questo punto possiamo definire la funzione inversa.
Siano A e B due sottoinsiemi impropri di R. Ovvero:
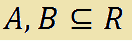
che si legge
A e B sottoinsiemi impropri di R.
E sia
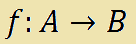
una FUNZIONE BIUNIVOCA.
Si chiama FUNZIONE INVERSA la funzione
f-1(y)
che si legge
f alla meno 1 di y
che associa ad ogni elemento y appartenente all'insieme B la sua controimmagine x appartenente all'insieme A.
Nelle prossime lezioni continueremo a parlare di funzioni inverse.






