COME RICONOSCERE SE UNA FUNZIONE E' SURRIETTIVA
- Funzioni reali di variabile reale
- Funzioni iniettive
- Come riconoscere se una funzione è iniettiva
- Come capire se una funzione è iniettiva
- Funzioni suriettive
- Funzioni biunivoche
- Come riconoscere se una funzione è biunivoca
- Rette parallele
Nella lezione precedente abbiamo detto che, se OGNI ELEMENTO di Y è IMMAGINE di ALMENO UN ELEMENTO di X la funzione prende il nome di FUNZIONE SURIETTIVA.
Ora, cerchiamo di capire come possiamo stabilire, esaminando il grafico di una funzione, se essa è SURIETTIVA o meno.
Esempio:
esaminiamo la funzione disegnata in basso.
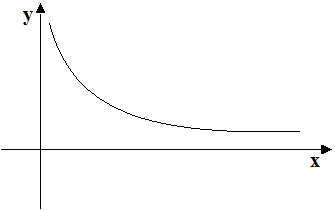
Al fine di stabilire se la FUNZIONE è SURIETTIVA o meno utilizziamo il TEST DELLE RETTE ORIZZONTALI, in altre parole disegniamo tante RETTE PARALLELE all'ASSE DELLE ASCISSE.
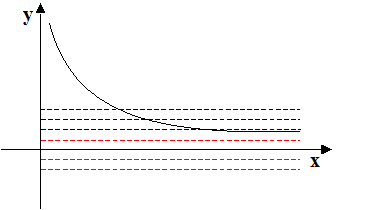
Se almeno una delle rette che abbiamo disegnato, NON INTERSECA IL GRAFICO della funzione in ALCUN PUNTO significa che la funzione NON E' SURIETTIVA dato che esiste almeno un valore di Y che non è immagine di nessun valore di X.
Ad esempio, la funzione da noi disegnata non è suriettiva poiché le rette parallele all'asse delle x che abbiamo disegnato in rosso non intersecano la funzione in nessun punto.






