FUNZIONE PARTE FRAZIONARIA
- Funzioni reali di variabile reale
- Funzione a scala
- Campo di esistenza delle funzioni
- L'insieme dei numeri reali
- Intervalli
Esaminiamo la seguente FUNZIONE
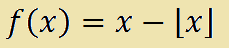
che si legge
f di x uguale a x meno la parte intera di x.
Questa funzione viene detta FUNZIONE PARTE FRAZIONARIA o FUNZIONE DECIMALE o ancora FUNZIONE MANTISSA.
Vediamo come costruire il grafico di questa funzione che risulta essere un po' particolare.
Innanzitutto diciamo che il campo di esistenza di questa funzione è dato dall'insieme dei numeri reali.
Assegniamo dei valori arbitrari alla x e vediamo quali valori assume la y.
| x | y | |
|---|---|---|
| -1,0 | -1 - 1 | 0 |
| -0,9 | -0,9 - 1 | 0,1 |
| -0,8 | -0,8 - 1 | 0,2 |
| -0,7 | -0,7 -1 | 0,3 |
| -0,6 | -0,6 - 1 | 0,4 |
| -0,5 | -0,5 -1 | 0,5 |
| -0,4 | -0,4 -1 | 0,6 |
| -0,3 | -0,3 - 1 | 0,7 |
| -0,2 | -0,2 -1 | 0,8 |
| -0,1 | -0,1 -1 | 0,9 |
| 0 | 0 - 0 | 0 |
| 0,1 | 0,1 - 0 | 0,1 |
| 0,2 | 0,2 - 0 | 0,2 |
| 0,3 | 0,3 - 0 | 0,3 |
| 0,4 | 0,4 - 0 | 0,4 |
| 0,5 | 0,5 - 0 | 0,5 |
| 0,6 | 0,6 - 0 | 0,6 |
| 0,7 | 0,7 - 0 | 0,7 |
| 0,8 | 0,8 - 0 | 0,8 |
| 0,9 | 0,9 - 0 | 0,9 |
| 1,00 | 1 - 1 | 0 |
Vediamo, graficamente, come si presenta questa funzione. Di seguito vi mostriamo due immagini dello stesso grafico: la prima evidenzia meglio i valori riportati sull'asse delle ascisse e su quello delle ordinate, la seconda fa capire meglio come si ripete il grafico.
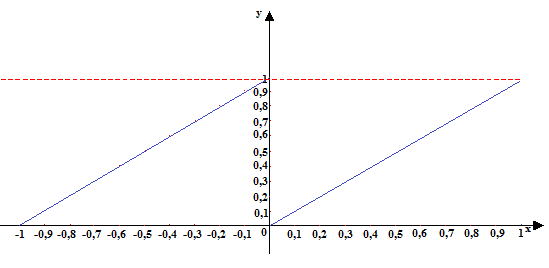
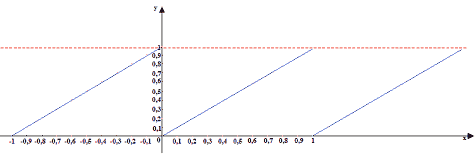
Come possiamo notare f(x) assume sempre valori compresi nell'intervallo
[0, 1[.






