FORMULA DI DUPLICAZIONE DELLA COTANGENTE
- Cotangente
- Formule goniometriche
- Formula di duplicazione del seno
- Formula di duplicazione del coseno
Nella lezione precedente abbiamo visto qual è la FORMULA DI DUPLICAZIONE DELLA COTANGENTE e come si giunge ad essa.
Sempre nella precedente lezione abbiamo detto che esiste un altro modo per dimostrare la formula di duplicazione della cotangente.
In questa lezione andremo a vedere questo secondo metodo.
Come sempre, iniziamo con lo scrivere:
cotg 2α
Noi sappiamo che la COTANGENTE di un angolo può essere espressa come il RAPPORTO tra il COSENO e il SENO dello stesso angolo. Quindi possiamo scrivere:
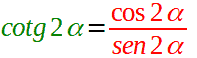
La formula di duplicazione del coseno ci dice che:
cos 2α = cos2 α - sen2 α
mentre la formula di duplicazione del seno ci dice che:
sen 2α = 2 sen α · cos α
Andando a sostituire queste due formule nella precedente, possiamo scrivere:
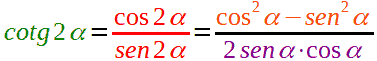
Ovviamente, trattandosi di una frazione, dobbiamo porre come condizione che il denominatore sia diverso da zero, affinché la frazione abbia significato. Quindi, la condizone da porre è:
2 sen α · cos α ≠ 0
Ovviamente questa condizione si verifica quando:
sen α ≠ 0
e
cos α ≠ 0
Affinché sen α sia diverso da 0 è necessario che:
α ≠ kπ
E affinché cos α sia diverso da 0 è necessario che:
α ≠ (π/2) + kπ
in entrambi i casi
con k ∈ Z
Ora torniamo alla nostra formula
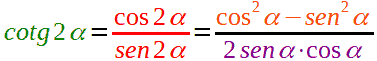
e andiamo a dividere, numeratore e denominatore, per sen2 α:
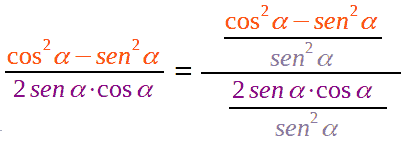
da cui otteniamo:
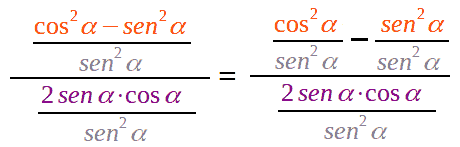
Semplificando, avremo:
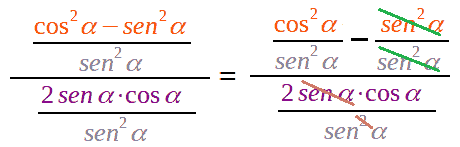
Poiché abbiamo diviso numeratore e denominatore per il sen2 α dobbiano porre come ulteriore condizione che:
sen2 α ≠ 0
che equivale a dire
sen α ≠ 0
ma questa condizione l'avevamo già posta in precedenza e quindi non è necessario riproporla.
Ora, ricordando che il rapporto tra il coseno e il seno di un angolo non è altro che la cotangente dell'angolo stesso, riscriviamo la formula di duplicazione della cotangente nel modo seguente:
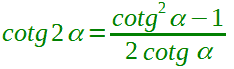
poste le seguenti condizioni di esistenza
α ≠ kπ
α ≠ (π/2) + kπ
con k ∈ Z
Ancora una volta si tratta esattamente della stessa formula a cui eravamo giunti nella precedente lezione.






