DISEQUAZIONI LOGARITMICHE CON UN LOGARITMO AD UN MEMBRO E LO ZERO ALL'ALTRO MEMBRO
- I logaritmi: definizione
- Logaritmi: casi particolari
- Disequazioni logaritmiche
- Risoluzione di disequazioni logaritmiche
- Disequazioni logaritmiche con due logaritmi aventi la stessa base
- Disequazioni logaritmiche risolvibili mediante i teoremi sui logaritmi
- Disequazioni logaritmiche con un logaritmo ad un membro ed una costante all'altro membro
- Disequazioni logaritmiche risolvibili mediante sostituzione
- Disequazioni logaritmiche risolvibili con il metodo grafico
Proseguiamo l'esame delle DISEQUAZIONI LOGARITMICHE.
In questa lezione ci occuperemo di quelle disequazioni nelle quali compaiono:
- un logaritmo a primo membro;
- lo zero a secondo membro.
Esse si presentano nella forma
loga f(x) ≥ 0
oppure
loga f(x) ≤ 0.
Chiaramente:
- al posto del segno ≥ possiamo trovare anche soltanto il segno di >;
- così come al posto del segno ≤ possiamo trovare anche soltanto il segno di<.
Andiamo ad esaminare la prima delle due disequazioni scritte: chiaramente il modo di procedere sarò lo stesso anche nel secondo caso.
La prima considerazione da fare è che l'ARGOMENTO di un LOGARITMO deve essere necessariamente MAGGIORE DI ZERO. Quindi sicuramente dovrà essere
f(x) > 0.
La seconda considerazione da fare è che noi sappiamo che il LOGARITMO dell'UNITA' è sempre uguale a ZERO. Cioè:
loga 1 = 0.
Questo significa che noi possiamo scrivere la nostra disequazione come
loga f(x) ≥ loga 1.
Come già abbiamo visto nelle lezioni precedenti (a cui si rimanda per una spiegazione più dettagliata), a questo punto entra in gioco la base a:
- se a > 1 andremo a risolvere la disequazione tra gli argomenti dei logaritmi avente lo STESSO VERSO;
- se 0 < a < 1 andremo a risolvere la disequazione tra gli argomenti dei logaritmi, avente VERSO CONTRARIO a quella fra i logaritmi.
Quindi, ricapitolando:
- se
a > 1
andremo a risolvere il sistema:
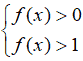
- se
0 < a < 1
andremo a risolvere il sistema:
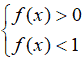
Esempio:
log(1/5) (4x+2) < 0.
La nostra disequazione può essere scritta come
log(1/5) (4x+2) < log(1/5) 1.
A questo punto possiamo risolvere.
Prima di tutto bisogna porre la condizione di esistenza, ovvero che l'argomento del logaritmo sia maggiore di zero, ovvero
4x + 2 > 0.
Poi dovremo risolvere la disequazione tra gli argomenti dei logaritmi. Dato che la base è compresa tra 0 e 1 dovremo cambiare il verso della disequazione, e scriveremo:
4x + 2 < 1.
Il sistema da risolvere sarà, quindi:
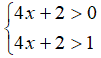
da cui avremo:
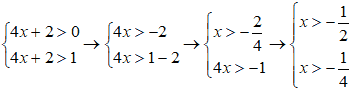
Graficamente avremo:
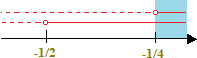
La soluzione cercata è data dalle
x > 1/4.






