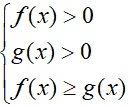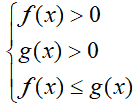RISOLUZIONE DI DISEQUAZIONI LOGARITMICHE
- I logaritmi: definizione
- Funzione logaritmica
- Disequazioni logaritmiche
- Disequazioni logaritmiche con due logaritmi aventi la stessa base
- Disequazioni logaritmiche risolvibili mediante i teoremi sui logaritmi
- Disequazioni logaritmiche con un logaritmo ad un membro e lo zero all'altro membro
- Disequazioni logaritmiche con un logaritmo ad un membro ed una costante all'altro membro
- Disequazioni logaritmiche risolvibili mediante sostituzione
- Disequazioni logaritmiche risolvibili con il metodo grafico
Iniziamo l'esame delle DISEQUAZIONI LOGARITMICHE.
In questa lezione ci occuperemo di quelle disequazioni nelle quali compaiono un logaritmo a primo membro e un logaritmo, avente la stessa base, a secondo membro.
In altre parole ci occuperemo di disequazioni del tipo:
loga f(x) ≥ loga g(x)
oppure
loga f(x) ≤ loga g(x).
Chiaramente:
- al posto del segno ≥ possiamo trovare anche soltanto il segno di >;
- così come al posto del segno ≤ possiamo trovare anche soltanto il segno di<.
La prima considerazione da fare è che l'ARGOMENTO di ciascun LOGARITMO presente nella disequazione deve essere necessariamente MAGGIORE DI ZERO come abbiamo appreso nelle lezioni precedenti. Quindi sicuramente dovrà essere
f(x) > 0
e
g(x) > 0.
Queste sono le CONDIZIONI DI ESISTENZA della nostra disequazione.
Ora, ricordiamo quello che abbiamo detto quanto abbiamo parlato delle equazioni logaritmiche sotto forma di uguaglianza di due logaritmi aventi la stessa base, cioè
loga f(x) = loga g(x).
Avevamo detto che, se i due logaritmi hanno la stessa base, è evidente che per essere uguali devono essere uguali anche gli argomenti, ovvero deve essere:
f(x) = g(x).
Per le disequazioni, però, la cosa diventa un po' più complessa, perché qui entra in gioco il valore della base a dei due logaritmi, che sappiamo deve essere sempre positiva. Studiando la funzione logaritmica abbiamo appreso che:
- se
la base è
a > 1
la funzione è CRESCENTE. Questo significa che, aumentando l'argomento aumenta anche il valore del suo logaritmo. Quindi, ad argomenti più grandi corrispondono logaritmi più grandi e viceversa.
Partiamo dalla disequazione del tipo
loga f(x) > loga g(x).
Essendo la funzione crescente possiamo dire che
se
loga f(x) > loga g(x)
sarà anche
f(x) > g(x).
Vediamo un esempio direttamente sul grafico della funzione logaritmica:
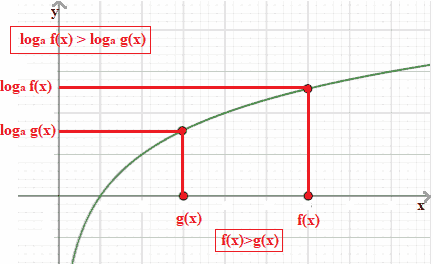
Passiamo ad esaminare la disequazione del tipo:
loga f(x) < loga g(x).
Essendo la funzione crescente possiamo dire che
se
loga f(x) < loga g(x)
sarà anche
f(x) < g(x).
Vediamolo graficamente:
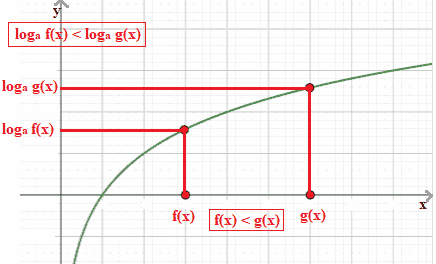
In altre parole quando
a > 1
scrivere la disequazione tra i due logaritmi è la stessa cosa che scrivere la disequazione tra i due argomenti, con lo stesso verso.
Chiaramente non cambierà nulla se, oltre al segno di maggiore o minore avremo anche il segno di uguale: basterà aggiungerlo.
-
se la base è
0 < a < 1
la funzione è DECRESCENTE. Questo significa che, aumentando l'argomento diminuisce il valore del suo logaritmo. Quindi, ad argomenti più grandi corrispondono logaritmi più piccoli e viceversa.
Partiamo dalla disequazione del tipo:
loga f(x) > loga g(x).
Essendo la funzione decrescente possiamo dire che
se
loga f(x) > loga g(x)
sarà
f(x) < g(x).
Vediamo, anche in questo caso, un esempio direttamente sul grafico della funzione logaritmica:
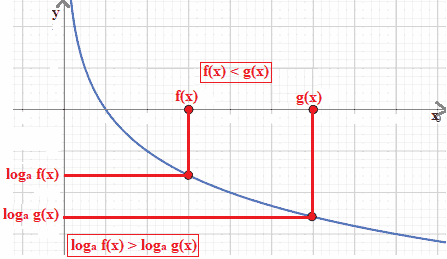
Passiamo alla disequazione del tipo
loga f(x) < loga g(x).
Essendo la funzione decrescente possiamo dire che
se
loga f(x) < loga g(x)
sarà
f(x) > g(x).
Lo possiamo, come sempre, vedere graficamente:
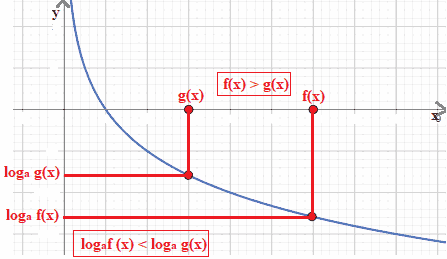
In altre parole quando
0 < a < 1
scrivere la disequazione tra i due logaritmi è la stessa cosa che scrivere la disequazione tra i due argomenti, con verso contrario a quella fra i logaritmi.
Anche in questo caso non cambierà nulla se, oltre al segno di maggiore o minore avremo anche il segno di uguale, che andremo ad aggiungere.
Quindi, ricapitolando, per risolvere una disequazione logaritmica del tipo appena visto si dovrà risolvere un sistema di disequazioni in cui porremo:
- le condizioni di esistenza della disequazione, ovvero che tutti gli argomenti dei logaritmi dati siano maggiori di zero;
- la
disequazione che si ottiene dalla disequazione degli argomenti:
- con lo stesso verso, se a > 1;
- con verso contrario , se 0 < a < 1.
In simboli possiamo scrivere:
| DISEQUAZIONE | a > 1 |
0 < a < 1 |
|---|---|---|
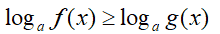 |
|
|
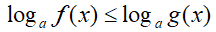 |
|
|
Nella prossima lezione vedremo alcuni esercizi nei quali applicheremo le regole appena apprese.