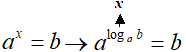LOGARITMI: CASI PARTICOLARI
Nella lezione precedente abbiamo detto che il LOGARITMO in base a di un numero b è l'ESPONENTE x da dare ad a per ottenere b, ponendo come condizioni che:
- a sia maggiore di zero e diverso da 1;
- e b sia maggiore di zero.
Dalla definizione di logaritmo sappiamo che:
- NON esistono logaritmi di BASE NEGATIVA, NULLA o UNITARIA;
- NON esistono logaritmi di ARGOMENTI NEGATIVI o NULLI.
Vediamo ora alcuni logaritmi particolari.
I CASO
Il LOGARITMO dell'UNITA' è sempre ZERO. Cioè:
loga 1 = 0.
Infatti si tratta di trovare il valore di x tale che elevando a ad x abbiamo come risultato 1:
ax = 1
ma questo valore è
x = 0
infatti, qualsiasi valore, elevato a zero dà come risultato 1.
II CASO
Il LOGARITMO in base a di a è uguale ad UNO. Cioè:
loga a = 1.
Infatti si tratta di trovare il valore di x tale che elevando a ad x abbiamo come risultato a:
ax = a
ma questo valore è
x = 1
infatti solamente elevando ad 1 un qualsiasi valore otteniamo se stesso.
III CASO
Esaminiamo un ulteriore caso particolare.
loga an = n.
Vediamo il perché.
Scrivere
loga an
significa cercare quel valore tale che, elevando a ad esso, otteniamo an ed è evidente che questo valore è n.
IV CASO
Infine diciamo che
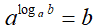
Vediamo il perché.
Noi sappiamo che, scrivere
loga b = x
equivale a dire che
ax = b.
Ora, se andiamo a sostituire alla x il corrispondente logaritmo, avremo: