EQUAZIONI LOGARITMICHE CON L'INCOGNITA NELLA BASE

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• I logaritmi: definizione
• Logaritmi: casi particolari
• Equazioni logaritmiche
• Equazioni logaritmiche sotto forma di uguaglianza di due logaritmi aventi la stessa base
• Equazioni logaritmiche sotto forma di uguaglianza di un logaritmo ed una costante
• Equazioni logaritmiche risolvibili mediante sostituzione
• Equazioni logaritmiche risolvibili con il metodo grafico
• Equazioni logaritmiche risolvibili con logaritmi aventi basi diverse
• Formula del cambiamento di base dei logaritmi
• Proprietà dei logaritmi derivate dalla formula di cambiamento di basi e dai teoremi sui logaritmi
• Tabella delle proprietà e dei teoremi dei logaritmi

Concludiamo l'esame dei metodi di risoluzione delle EQUAZIONI LOGARITMICHE parlando delle equazioni che contengono l'INCOGNITA nella BASE.

Imbattersi in questo tipo di equazioni non è molto frequente, e quando ci capiterà, molto probabilmente, si tratterà di equazioni non molto complesse.

Per risolvere questo tipo di equazioni occorrerà cercare di ricondurle ad una delle forma a noi note.

Qui esamineremo tre dei possibili modi in cui esse si possono presentare:

1° CASO

EQUAZIONE che contiene UN LOGARITMO, con l'incognita nella base, AD UN MEMBRO ed una COSTANTE ALL'ALTRO.

L'equazione assume la forma

log_f(x)k = h

con

k, h costanti.

Prima di procedere, dobbiamo porre come CONDIZIONE DI ESISTENZA che la BASE del logaritmo presente a primo membro sia MAGGIORE DI ZERO e DIVERSA da 1. Ricordiamo, infatti, che la base di un logaritmo non può mai essere negativa, né uguale all'unità.

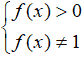
Quindi andremo a cercare la soluzione della nostra equazione ricorrendo alla DEFINIZIONE di LOGARITMO.

Da essa sappiamo che, se

log_a b = x

significa che

a^x = b.

Quindi, nel nostro esempio, avremo che:

f(x)^h = k.

A questo punto non ci resterà che risolvere.

Esempio:

log_x 9 = 2.

Poniamo le condizioni di esistenza:

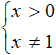
Quindi, ricorrendo alla definizione di logaritmo, possiamo scrivere:

x² = 9.

Poniamo sotto radice quadrata, primo e secondo membro, ed abbiamo:

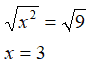
La soluzioni trovata è perfettamente compatibile con le condizioni di esistenza poste.

2° CASO

EQUAZIONE CHE SI PRESENTA IN FORMA DIVERSA RISPETTO ALLA PRECEDENTE.

Anche in questo caso bisogna porre la CONDIZIONE DI ESISTENZA che tutte le BASI dei logaritmi presenti nell'equazione siano MAGGIORI DI ZERO e DIVERSE da 1.

Una volta poste queste condizioni si tratterà, come sempre, di cercare di trasformare l'equazione in una delle forme note e procedere alla sua soluzione. Spesso può essere utile l'uso della formula del cambiamento di base dei logaritmi.

Esempio:

log_(x+1) 30 = log₅ 20.

Iniziamo col porre le condizioni di esistenza, ovvero che la base del logaritmo sia maggiore di zero e diversa da 1:

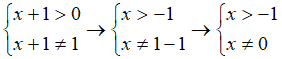
Ora applichiamo la formula del cambiamento di base dei logaritmi:

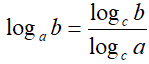
e scriviamo il logaritmo in base x+1 come logaritmo in base 5:

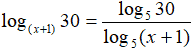
Sostituiamo nell'equazione e scriviamo:

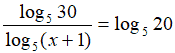
Possiamo tranquillamente compiere questo passaggio dato che abbiamo posto nelle CONDIZIONI DI ESISTENZA che

x + 1 ≠ 1.

Perché questo?

Perché, solamente nel caso in cui l'argomento del logaritmo è pari ad 1 (qualunque sia la sua base), il logaritmo è pari a zero e, quindi, il nostro denominatore sarebbe uguale a zero. Ma dato che noi abbiamo posto nelle condizioni di partenza che

x + 1 ≠ 1

sicuramente il suo logaritmo sarà diverso da zero.

Ora dobbiamo togliere l'incognita dal denominatore: lo facciamo moltiplicando entrambi i membri per

log₅ (x+1)

in modo da ottenere:

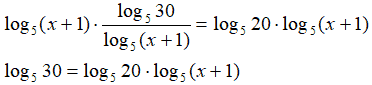
A questo punto dividiamo, primo e secondo membro, per

log₅ 20

in modo da isolare il logaritmo contenente l'incognita nell'argomento:

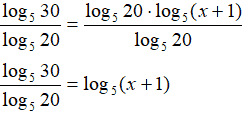
Notiamo che, a primo membro abbiamo il rapporto tra due logaritmi che hanno come argomento, entrambi, un numero: quindi abbiamo un numero. Di conseguenza, la nostra equazione è riconducibile al caso in cui abbiamo ad un membro un logaritmo e all'altro membro una costante e, come sappiamo, questo tipo di equazioni si risolvono ricorrendo alla definizione di logaritmo.

Scriviamo l'equazione appena vista nella forma a noi più nota, per cercare di non confonderci troppo le idee:

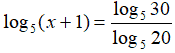
Come abbiamo ripetuto più volte, dire che

log_a b = x

significa che

a^x = b.

Quindi, nel nostro esempio, avremo che:

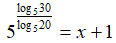
Per trovare il valore della x, portiamo a primo membro l'1, cambiandogli di segno:

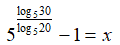
Abbiamo così determinato il valore della nostra x.

Ora, andiamo a verificare che la soluzione trovata sia accettabile in base alle condizioni di esistenza dell'equazione poste inizialmente, ovvero che essa sia maggiore di -1 e diverso da zero.

Il logaritmo in base 5 di 30 è all'incirca pari a 2,11.

Il logaritmo in base 5 di 20 è all'incirca pari a 1,86.

Il loro rapporto è pari a 1,13: quindi un valore superiore all'unità.

Elevando il 5 ad un valore superiore ad 1 otteniamo un numero maggiore di 5. Quindi, se sottraiamo 1, abbiamo senz'altro un valore maggiore di -1 e diverso da zero, di conseguenza il risultato ottenuto è accettabile.

3° CASO

EQUAZIONE CHE CONTIENE L'INCOGNITA SIA NELLA BASE CHE NELL'ARGOMENTO.

Potrebbe accadere che l'equazione contenga l'INCOGNITA non solo nella BASE, ma anche nell'ARGOMENTO. In questo caso dobbiamo porre come CONDIZIONI DI ESISTENZA non solo che le BASI di tutti i logaritmi presenti nell'equazione siano MAGGIORI DI ZERO e DIVERSE da 1, ma anche che gli ARGOMENTI contenenti l'incognita siano MAGGIORI DI ZERO.

Il passo successivo sarà quello di cercare di eliminare l'incognita dalla base del logaritmo utilizzando opportunamente la FORMULA DEL CAMBIAMENTO DI BASE DEI LOGARITMI.

Esempio:

log_x (x + 6) = 2.

L'incognita è presente sia nella base del logaritmo che nell'argomento. Andiamo a porre allora come condizioni che la base sia maggiore di zero e diversa da 1 e l'argomento sia maggiore di zero. Quindi le condizioni di esistenza sono date dal sistema:

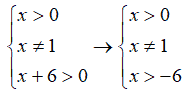
Graficamente abbiamo:

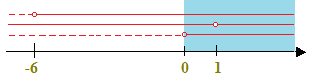
Quindi, affinché la soluzione sia valida è necessario che essa sia maggiore di zero e diversa da 1.

A questo punto usiamo la formula del cambiamento della base del logaritmo, in modo da trasformare il nostro logaritmo in base x in un logaritmo che non contenga l'incognita nella base: la scelta è arbitraria. Noi scegliamo il logaritmo naturale.

Quindi la formula

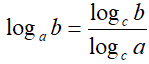
nel nostro caso diventa:

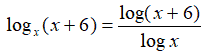
Sostituendo nella nostra equazione di partenza avremo:

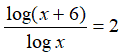
Ora dobbiamo togliere l'incognita dal denominatore e lo facciamo moltiplicando, primo e secondo membro, per il logaritmo di x:

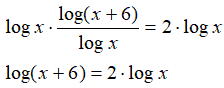
Applicando il teorema della potenza di un logaritmo, possiamo scrivere:

log (x + 6) = log x².

A questo punto abbiamo un'equazione con un logaritmo a primo membro, ed un logaritmo, avente la stessa base, a secondo membro. Essa si risolve eguagliando gli argomenti, ovvero:

x + 6 = x².

Portiamo x² al primo membro cambiando di segno e risolviamo:

- x² + x + 6 = 0

x² - x - 6 = 0

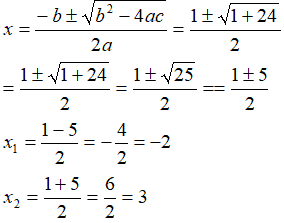
Mettiamo a confronto le due soluzioni ottenute con le condizioni di esistenza dell'equazione: avevamo detto che la soluzione trovata sarebbe stata ammissibile solamente se maggiore di zero e diversa da 1. E' chiaro, allora, che la prima soluzione non è ammissibile.

Quindi il risultato della nostra equazione è

x = 3.

Lezione precedente - Lezione successiva

Indice degli argomenti su esponenziali e logaritmi

Pubblicità/Advertising