PROPRIETA' DEI LOGARITMI DERIVATE DALLA FORMULA DI CAMBIAMENTO DI BASI E DAI TEOREMI SUI LOGARITMI
- I logaritmi: definizione
- Logaritmi: casi particolari
- Teoremi sui logaritmi: teorema della potenza di un logaritmo
- Formula del cambiamento di base dei logaritmi
- Proprietà dei logaritmi derivate dai teoremi sui logaritmi
- Inverso di una frazione
Continuiamo a parlare delle PROPRIETA' dei LOGARITMI: in questa lezione ci occuperemo di una serie di proprietà che possono essere desunte dalla formula di cambiamento di basi e dai teoremi sui logaritmi.
I PROPRIETA'
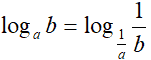
Dimostriamo questa proprietà. Partiamo da
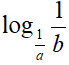
Applichiamo la formula del cambiamento di basi e trasformiamo il logaritmo in base 1/a in un logaritmo in base a:
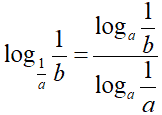
Ma
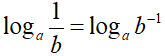
e per il teorema della potenza di un logaritmo possiamo scrivere:
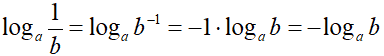
Allo stesso modo avremo:
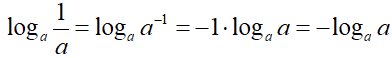
Ma noi sappiamo che
Quindi
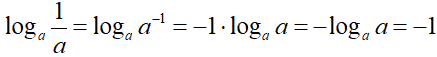
Di conseguenza
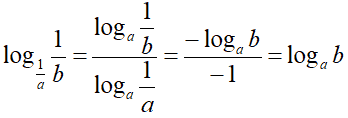
Quindi per trasformare un logaritmo in un altro logaritmo che abbia l'INVERSO della BASE del logaritmo di partenza, occorre INVERTIRE anche l'ARGOMENTO.
II PROPRIETA'
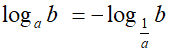
Vediamo il perché. Andiamo ad applicare la formula del cambiamento di basi e trasformiamo il logaritmo in base 1/a in un logaritmo in base a:
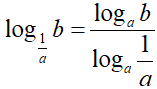
Abbiamo già visto che:
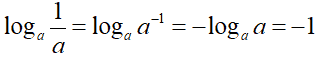
quindi
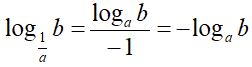
Allo stesso modo avremo:
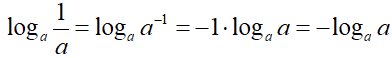
Ma noi sappiamo che
Quindi
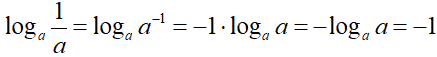
Di conseguenza
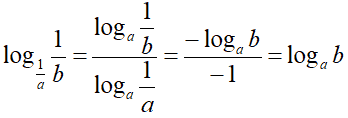
Un altro modo per trasformare un logaritmo in un altro logaritmo che abbia l'INVERSO della BASE del logaritmo di partenza, è quello di CAMBIARE di SEGNO al logaritmo.
III PROPRIETA'
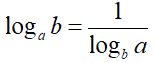
Applichiamo la formula del cambiamento di basi e trasformiamo il logaritmo in base a in un logaritmo in base b:
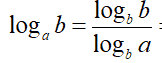
Ma dato che:
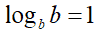
avremo
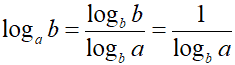
Quindi possiamo dire che per trasformare un logaritmo in un altro logaritmo in cui siano tra loro SCAMBIATE la BASE con l'ARGOMENTO, occorre porre il nuovo logaritmo a DENOMINATORE di una frazione al cui nominatore c'è l'unità.
IV PROPRIETA'
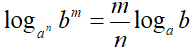
Applichiamo la formula del cambiamento di basi e trasformiamo il logaritmo in base an in un logaritmo in base a:
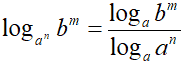
Applichiamo, a numeratore e a denominatore, il teorema della potenza di logaritmi e scriviamo:
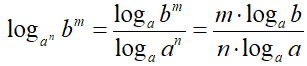
Ricordando che
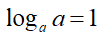
avremo:
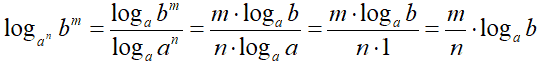
Quindi, se abbiamo un logaritmo in cui BASE e ARGOMENTO sono due POTENZE possiamo scrivere il logaritmo come il PRODOTTO tra, una frazione che abbia a NUMERATORE l'ESPONENTE dell'ARGOMENTO e a DENOMINATORE l'ESPONENTE della BASE, e il logaritmo di partenza privato degli esponenti.






