EQUAZIONI LOGARITMICHE SOTTO FORMA DI UGUAGLIANZA DI UN LOGARITMO E DI UNA COSTANTE
- I logaritmi: definizione
- Logaritmi: casi particolari
- Equazioni logaritmiche
- Equazioni logaritmiche sotto forma di uguaglianza di due logaritmi aventi la stessa base
- Equazioni logaritmiche risolvibili mediante sostituzione
- Equazioni logaritmiche risolvibili con il metodo grafico
- Equazioni logaritmiche risolvibili con logaritmi aventi basi diverse
- Equazioni logaritmiche con l'incognita nella base
- Tabella delle proprietà e dei teoremi dei logaritmi
- Teoremi sui logaritmi: teorema sul rapporto di logaritmi
Proseguiamo il nostro esame sui metodi di risoluzione delle EQUAZIONI LOGARITMICHE per vedere come procedere nel caso in cui l'equazione, mediante la definizione stessa di logaritmo o mediante le proprietà e i teoremi dei logaritmi,può essere ricondotta alla forma
loga f(x) = k
con
k costante.
In pratica ci troviamo con un'equazione che ha, ad un membro un logaritmo, e all'altro membro una costante (k).
Per risolvere questo tipo di equazione ricorriamo alla DEFINIZIONE di LOGARITMO.
Noi sappiamo che, se
loga b = x
significa che
ax = b.
Quindi
loga f(x) = k
può essere scritto come
ak = f(x).
Ovviamente la condizione è sempre che
a > 0
e
a ≠ 1.
Così come abbiamo visto nella lezione precedente, anche in questo caso, dovremo fare attenzione perché le soluzioni ottenute potrebbero non essere anche soluzioni della equazione logaritmica di partenza, infatti,tutti gli argomenti dei logaritmi presenti nella equazione di partenza devono essere maggiori di zero.
Quindi, così come abbiamo visto nella lezione precedente, possiamo procedere in due modi diversi:
- possiamo risolvere l'equazione
ak = f(x)
e successivamente andare a SOSTITUIRE i VALORI TROVATI nell'equazione di partenza
loga f(x) = k
in modo da verificare che i logaritmi ottenuti siano validi. Se, in seguito alla sostituzione, anche uno solo degli argomenti non è positivo, la soluzione non è accettabile;
- oppure possiamo determinare il CAMPO
DI ESISTENZA dell'equazione risolvendo un SISTEMAformato
da tante DISEQUAZIONI quanti sono
i logaritmi presenti nell'equazione. Ogni equazione dovrà porre la
condizione che l'ARGOMENTO di
ciascun logaritmo sia POSITIVO.
Le soluzioni dell'equazione
ak = f(x)
possono essere accettate solamente se appartengono al campo di esistenza.
Esempio:
log2 (3x-2) - 3 = log2 10x - log2 5x.
Iniziamo col trasformare l'equazione applicando la definizione di logaritmo e le proprietà e i teoremi sui logaritmi.
A secondo membro, applichiamo il TEOREMA SUL RAPPORTO DI LOGARITMI:
log2 (3x-2) - 3 = log2 (10x/ 5x)
da cui otteniamo
log2 (3x-2) - 3 = log2 2.
E poiché
possiamo scrivere:
log2 (3x-2) - 3 = 1
da cui, portando il -3 a secondo membro e cambiando di segno, otteniamo:
log2 (3x-2) = 1 + 3
log2 (3x-2) = 4.
Abbiamo così un'equazione nella quale compare un logaritmo a primo membro ed una costante a secondo membro.
Ora passiamo, usando la definizione di logaritmo, all'esponenziale e scriviamo:
24 = 3x - 2.
A questo punto possiamo seguire due strade:
- la prima consiste nel trovare la soluzione e sostituirla nell'equazione di partenza per verificare che l'argomento di tutti i logaritmi sia positivo;
- la seconda consiste nel determinare a priori il campo di esistenza dell'equazione, quindi risolverla e vedere se la soluzione trovata rientra in tale campo di esistenza.
Seguiamo questa seconda soluzione.
Il campo di esistenza dell'equazione lo si ottiene risolvendo il seguente sistema:
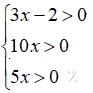
dal quale otteniamo:
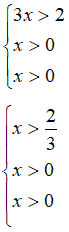
Graficamente abbiamo:
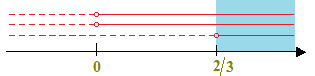
Quindi il sistema ammette soluzioni per le
x > 2/3.
Di conseguenza, solamente se la x è maggiore di 2/3 l'argomento di tutti i logaritmi è positivo.
A questo punto possiamo andare a risolvere l'equazione ottenuta passando all'esponenziale, ovvero:
24 = 3x - 2.
Da cui otteniamo:
16 = 3x - 2
-3x = -2 - 16
3x = 2 + 16
3x = 18
x = 18/3 = 6.
Essendo 6 maggiore di 2/3, la soluzione è accettabile.






