EQUAZIONI RICONDUCIBILI AD EQUAZIONI OMOGENEE DI SECONDO GRADO IN SENO E COSENO
- Equazioni omogenee di secondo grado in seno e coseno
- Esempi di risoluzione di equazioni omogenee di secondo grado in seno e coseno
- Prima relazione fodamentale della goniometria
In questa lezione andremo a vedere un tipo di EQUAZIONI GONIOMETRICHE che possono essere risolte trasformandole in EQUAZIONI OMOGENEE DI SECONDO GRADO IN SENO E COSENO.
Le equazioni di cui stiamo parlando si presentano nella forma:
a sen2 x + b sen x cos x + c cos 2 x = d
Ricordiamo che le equazioni omogenee di secondo grado in seno e coseno si presentano nella forma
a sen2 x + b sen x cos x + c cos 2 x = 0
Quindi, la differenza tra queste due equazioni sta nel TERMINE NOTO che, nella equazione omogenea di secondo grado in seno e coseno, è pari a zero:
a sen2 x + b sen x cos x + c cos 2 x = d
a sen2 x + b sen x cos x + c cos 2 x = 0
Vediamo come è possibile trasformare questo tipo di equazione in modo da ricondurla ad una'equazione omogenea di secondo grado in seno e coseno.
Partiamo dall'equazione che dobbiamo risolvere:
a sen2 x + b sen x cos x + c cos 2 x = d
La PRIMA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA ci dice che
sen2 x + cos2 x = 1
Andiamo, quindi, a moltiplicare d per sen2 x + cos2 x: poiché la somma del sen2 x + cos2 x è uguale ad 1, effettuare questo prodotto significa moltiplicare d per 1 e, di conseguenza, l'equazione non cambia:
a sen2 x + b sen x cos x + c cos 2 x = d (sen2 x + cos2 x )
da cui ricaviamo:
a sen2 x + b sen x cos x + c cos 2 x = d sen2 x + d cos2 x
A questo punto si tratterà semplicemente di eseguire i calcoli e ci troveremo a dover risolvere un'EQUAZIONE OMOGENEA DI SECONDO GRADO IN SENO E COSENO. Iniziamo col portare tutti i termini a primo membro cambiando loro di segno:
a sen2 x + b sen x cos x + c cos 2 x - d sen2 x - d cos2 x = 0
Mettiamo in evidenza il seno e il coseno di x ed otteniamo:
(a - d) sen2 x + b sen x cos x + (c - d) cos 2 x = 0
Abbiamo così trasformato la nostra equazione in un'EQUAZIONE OMOGENEA DI SECONDO GRADO IN SENO E COSENO.
Esempio:
2 sen2 x + 3 sen x cos x - cos2 x = 2.
Nel nostro esempio:
d = 2
Moltiplichiamo 2 per (sen2 x + cos2 x) ed abbiamo:
2 sen2 x + 3 sen x cos x - cos2 x = 2 (sen2 x + cos2 x)
Eseguiamo la moltiplicazione a secondo membro:
2 sen2 x + 3 sen x cos x - cos2 x = 2 sen2 x + 2 cos2 x
Semplifichiamo e sommiamo i termini simili a primo e secondo membro:
2 sen2 x + 3 sen x cos x - cos2 x = 2 sen2 x + 2 cos2 x
-3 cos2 x + 3 sen x cos x = 0.
Quella che abbiamo scritto è un'EQUAZIONE OMOGENEA DI SECONDO GRADO IN SENO E COSENO con a = 0.
Ora possiamo mettere in evidenza 3 cos x:
3 cos x (- cos x + sen x) = 0
Per la legge di annullamento del prodotto le soluzioni dell'equazione sono:
3 cos x = 0
oppure
- cos x + sen x = 0
o entrambe nulle.
Dalla prima equazione ricaviamo come soluzione
x = π/2 + kπ
La seconda equazione è un'equazione linerare in seno e coseno in cui il termine noto è uguale a zero. Essa si risolve dividendo tutti i membri per cos x:
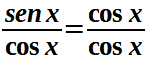
da cui si ottiene:
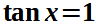
la cui soluzione è
x = π/4 + kπ.
Quindi le soluzioni trovare sono:
x = π/2 + kπ ∨ x = π/ + kπ
con






