EQUAZIONI GONIOMETRICHE RICONDUCIBILI AD EQUAZIONI ELEMENTARI DEL TIPO
cos x = b
- Equazioni goniometriche
- Equazioni goniometriche elementari del tipo cos x = b
- Esempi di risoluzione di equazioni goniometriche elementari del tipo cos x = b
Nelle lezioni precedenti abbiamo visto, attraverso alcuni esempi, come si risolvono le EQUAZIONI GONIOMETRICHE ELEMENTARI del tipo
cos x = b
che prendono il nome di EQUAZIONI GONIOMETRICHE ELEMENTARI NEL COSENO.
Ora vogliamo occuparci di alcune equazioni goniometriche che, pur non presentandosi in questo modo, sono facilmente RICONDUCIBILI ad essa.
Esempio 1:
2 cos x = 1
Se ricordate quanto abbiamo detto nella risoluzione delle equazioni riconducibili alle equazioni goniometriche elementari nel seno vi sarà chiaro che per risolvere questa equazione dobbiamo semplicemente DIVIDERE primo e secondo membro per il numero per il quale viene moltiplicato il coseno, ovvero per 2.
Quindi, scriveremo:
2 cos x = 1
cos x = 1/2
Abbiamo così ottenuto una normale equazione goniometrica elementare nel coseno.
Poiché il valore di b è compreso tra -1 e +1 (essendo uguale ad 1/2), la nostra equazione ammette soluzioni.
Noi sappiamo che le soluzioni sono:
x = ± α +2kπ
Nel nostro caso, 1/2 è il coseno di un arco noto ovvero π/3. Quindi la nostra soluzione sarà:
x = ± π/3 +2kπ
con
Ovviamente possiamo sempre scrivere il risultato in gradi sessadecimali, ovvero:
x = ± 60° +k·360°
con
Esempio 2:
cos 3x = -1/2
Questa equazione differisce dall'equazione goniometrica elementare nel coseno vista in precedenza perché l'angolo di cui conosciamo il coseno non è x, bensì 3x:
Per risolverla, quindi, dobbiamo considerare che 3x è il nostro angolo e successivamente dobbiamo trovare il valore di x.
Prima di tutto, iniziamo col verificare che la nostra equazione ammetta soluzioni: e così è essendo b = - 1/2.
L'arco il cui coseno è pari a -1/2 è 2π/3.
Quindi possiamo scrivere:
3x = ± 2π/3 +2kπ
A questo punto, per trovare il valore di x non ci resta che dividere primo e secondo membro per 3.
Quindi, avremo:
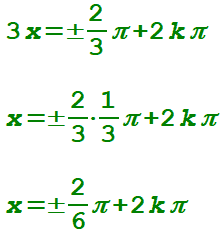
con






