PUNTI IN COMUNE A DUE CIRCONFERENZE
- Equazione della circonferenza
- Posizioni reciproche di due circonferenze
- Sistemi di equazioni di grado superiore al primo
- Grado di un sistema di equazioni
- Principio di riduzione di un sistema
- Metodo di riduzione
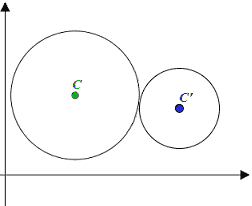
Dallo studio della circonferenza sappiamo che DUE CIRCONFERENZE possono essere tra loro:
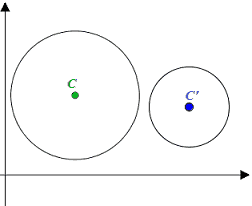
- una ESTERNA
all'altra;
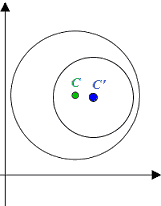
- una INTERNA
all'altra;
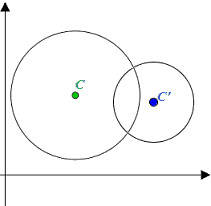
- SECANTI;
- TANGENTI che a loro volta possono essere:
-
interne
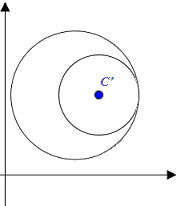
- o esterne
-
interne
- CONCENTRICHE
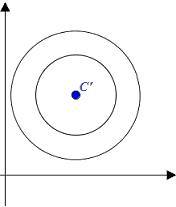
Quindi possiamo dire che, date DUE CIRCONFERENZE, esse hanno dei PUNTI in COMUNE solamente se sono:
- SECANTI. In questo caso hanno DUE PUNTI in COMUNE;
- TANGENTI, sia INTERNE che ESTERNE. In questo caso hanno UN solo PUNTO in COMUNE.
Ora, se ci vengono date le equazioni di due circonferenze e vogliamo trovare, se vi sono, i loro punti in comune dobbiamo mettere a SISTEMA le equazioni delle due circonferenze. I valori che soddisfano entrambe le equazioni rappresentano i punti in comune.
Indichiamo l'equazione della prima circonferenza con:
x2 + y2 + a1x + b1y + c1 = 0
e l'equazione della seconda circonferenza con:
x2 + y2 + a2x + b2y + c2 = 0.
Mettiamo a sistema le due equazioni
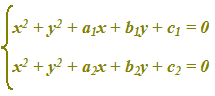
Questo sistema è però di 4° grado e dunque di difficile soluzione.
Se le due circonferenze non sono concentriche, applichiamo il metodo di riduzione per la risoluzione del sistema: metodo che si basa sul principio di riduzione di un sistema. Il metodo consiste nel sostituire ad una equazione del sistema, l'equazione che si ottiene sottraendo (o sommando) membro a membro tutte le equazioni del sistema.
Ovviamente, poiché siamo in grado di trovare il centro delle due circonferenze, conoscendo la loro equazione, siamo in grado di sapere se esse sono concentriche e se sono concentriche siamo sicuri che esse non hanno nessun punto in comune.
Noi scegliamo la sottrazione in modo da semplificare il sistema.
Quindi SOTTRAENDO MEMBRO A MEMBRO avremo:
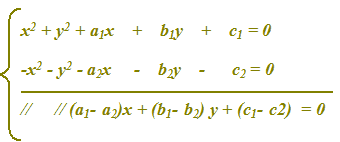
Se le due circonferenze fossero concentriche, sarebbero uguali anche i valori di a e di b e sottraendoli membro a membro i termini (a1 - a2)x e (b1 - b2)y si annullerebbero: per questo il metodo non è applicabile.
A questo punto abbiamo ottenuto una equazione di primo grado.
Scriviamo, allora, un SISTEMA con:
- una delle due equazioni della circonferenza (noi abbiamo scelto la prima, come potete vedere sotto, ma si poteva scegliere anche la seconda);
- l'equazione di primo grado appena ottenuta.
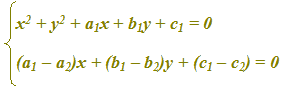
Risolviamo il sistema e otterremo i punti in comune alle due circonferenze. In particolare avremo:
- il SISTEMA NON
ammette SOLUZIONI. Ciò si
verifica quando le due circonferenze sono:
- una ESTERNA all'altra;
- una INTERNA all'altra;
- il SISTEMA
ammette UNA sola
SOLUZIONE. Ciò si verifica quando le due circonferenze
sono:
- TANGENTI INTERNE;
-
TANGENTI ESTERNE;
- il SISTEMA ammette DUE SOLUZIONI. Ciò si verifica quando le due circonferenze sono SECANTI.
Esempio:
date le circonferenze di equazione x2 + y2 - 12x - 4y + 31 = 0 e x2 + y2 -12x +6y + 41 = 0 dire se esse hanno dei punti in comune e se si quali sono le loro coordinate.
Innanzitutto possiamo dire che le due circonferenze sicuramente non sono concentriche (infatti a1 è uguale ad a2, ma b1 e b2 sono diversi).
Mettiamo a sistema le due equazioni
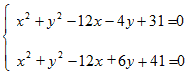
Sottraiamo, membro a membro, alla prima equazione la seconda equazione:
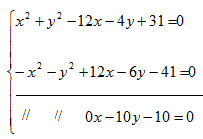
Mettiamo a sistema l'equazione appena trovata con la prima:
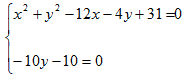
Ricaviamo dalla seconda il valore della y. E avremo:
-10y - 10 = 0
10y + 10 = 0
10y = -10
y= -1.
Sostituiamo il valore ottenuto della y nella prima equazione:
x2 + y2 - 12x - 4y + 31 = 0
x2 + 1 - 12x + 4 + 31 = 0.
Ricaviamo il valore della x:
x2 + 1 - 12x + 4 + 31 = 0
x2 - 12x + 36 = 0
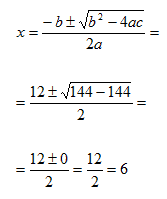
Quindi abbiamo una sola soluzione, il che vuol dire che le due circonferenze sono tangenti. Il punto di tangenza è dato da:
P (6 ; -1).






