CAMPO DI ESISTENZA DELLE FUNZIONI
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- Funzioni reali di variabile reale
- Classificazione delle funzioni reali
- Dominio di una funzione algebrica razionale intera
- Dominio di una funzione algebrica razionale fratta
- Dominio di una funzione algebrica irrazionale intera
- Dominio di una funzione algebrica irrazionale fratta
- Dominio di una funzione esponenziale
- Dominio di una funzione logaritmica
- Dominio di una funzione trigonometrica
- L'insieme dei numeri reali
- L'insieme dei numeri razionali relativi
Ricapitoliamo, con l'aiuto di una tabella, quanto abbiamo visto nelle lezioni precedenti.
FUNZIONE |
TIPO |
CONDIZIONE DA PORRE PER LA RICERCA DEL CAMPO DI ESISTENZA |
|---|---|---|
| Razionale intera | y = P(x) | nessuna |
| Razionale fratta | y=P(x)/P'(x) | P'(x) ≠
0 |
| Irrazionale intera | 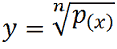 |
n dispari - nessuna |
| n pari - P(x)
≥ 0 |
||
| Irrazionale fratta | 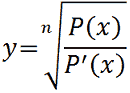 |
n dispari - P'(x) ≠
0 |
| n pari
- P(x)/P'(x) ≥
0 e P'(x) ≠ 0 |
||
| Esponenziale | y = ax | nessuna |
| y = aP(x) | condizione
di esistenza di P(x) |
|
| Logaritmiche | y = log x | x >
0 |
| y = log P(x) | P(x)
> 0 |
|
| Trigonometriche | y = sin x | nessuna |
| y = cos x | nessuna |
|
| y = tg x | 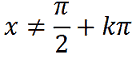 con k appartenente ai numeri interi |
|
| y = ctg x | 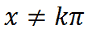 con k appartenente ai numeri interi |
|
| y = arcsin x | -1
≤ x ≤ +1 |
|
| y = arccos x | -1
≤ x ≤ +1 |
Quando cerchiamo il CAMPO DI ESISTENZA di una FUNZIONE dobbiamo ricordare che se occorre porre PIU' CONDIZIONI DI ESISTENZA esse vanno MESSE A SISTEMA tra loro.






