RAPPRESENTAZIONE GRAFICA DI UN'EQUAZIONE DI PRIMO GRADO
- Equazione della retta
- Rappresentazione grafica di una funzione
- Identità ed equazioni
- Equazione di primo grado ad una incognita
- Radici di una equazione
- Come si risolve una equazione di primo grado in una incognita
In questa lezione cercheremo di capire come possiamo applicare quanto appreso nelle lezioni precedente nella soluzione di un'equazione di primo grado. In particolare vedremo come è possibile determinare GRAFICAMENTE la RADICE di un'EQUAZIONE di PRIMO GRADO.
Consideriamo la seguente equazione:
2x + 4 = 0.
Vediamo come è possibile risolverla graficamente.
Per prima cosa UGUAGLIAMO ad y il PRIMO MEMBRO dell'equazione. In altre parole poniamo
2x + 4
uguale ad y.
Quindi, scriveremo:
y = 2x + 4.
Quella che abbiamo scritto è L'EQUAZIONE di una RETTA.
Ora, andiamo a DISEGNARE la nostra RETTA.
| x | y |
|---|---|
| 0 | 4 |
| 1 | 6 |
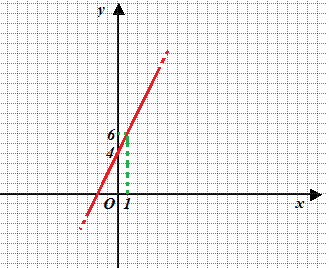
Ora osserviamo il punto P:
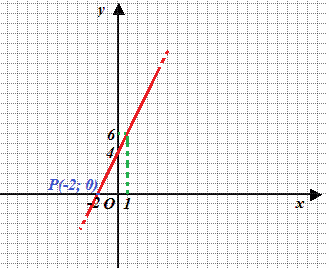
Esso individua il punto di intersezione della nostra retta con l'asse delle x, ovvero il punto in cui la y è uguale a zero. La y è uguale a zero quando la x è uguale a -2. Ma, -2, non è altro che la RADICE dell'equazione, cioè quel valore che soddisfa la nostra equazione. Infatti noi stavamo cercando i valori di x per i quali l'equazione è uguale a zero e ciò accade, appunto, quando essa è pari a -2.
Facciamo una prova. Risolviamo normalmente la nostra equazione. Avremo:
2x + 4 = 0
2x = - 4
x = -4/2 = -2.
Esattamente come volevamo dimostrare.
Vediamo un secondo esempio.
Data l'equazione
6x - 3 = 0.
vogliamo risolverla graficamente.
Andiamo ad UGUAGLIARE ad y il PRIMO MEMBRO dell'equazione:
y = 6x - 3.
e andiamo a DISEGNARE la RETTA:
| x | y |
|---|---|
| 0 | -3 |
| 1 | 3 |
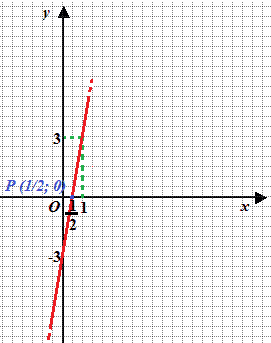
Il punto P ha coordinate 1/2 e 0. Esso individua la radice dell'equazione che è, appunto, 1/2.
Facciamo, anche in questo caso, la prova e risolviamo normalmente la nostra equazione:
6x - 3 = 0
6x = 3
x = 3/6 = 1/2.
La soluzione trovata è la stessa.






