ESERCIZI SUI FASCI DI CIRCONFERENZE
- Equazione della circonferenza
- Punti in comune a due circonferenze
- Asse radicale di due circonferenze
- Costruzione dell'asse radicale di due circonferenze esterne
- Fascio di circonferenze proprio e improprio
- Equazione del fascio di circonferenze
- Vari tipi di fasci di circonferenze
- Bisettrice del primo e terzo quadrante
Nelle lezioni precedenti abbiamo visto cos'è un FASCIO di CIRCONFERENZE, qual è l'EQUAZIONE del FASCIO di CIRCONFERENZE e i VARI TIPI di FASCI di CIRCONFERENZE.
Ora vedremo come le nozioni apprese possono essere applicate nella soluzione di alcuni esercizi.
Esercizio 1:
dato il fascio di circonferenze di equazione x2 + y2 + (k - 6)x + (6 - k)y + 9 - 3k = 0 dire per quali valori di k si ottiene l'equazione della circonferenza del fascio passante per il punto P(1;2).
Per risolvere l'esercizio è sufficiente porre, nell'equazione del fascio di circonferenze
x = 1
y = 2
e trovare il valore di k.
Pertanto avremo:
x2 + y2 + (k - 6)x + (6 - k)y + 9 - 3k = 0
12 + 22 + (k - 6)1 + (6 - k)2 + 9 - 3k = 0
1 + 4 + k - 6 + 12 - 2k + 9 - 3k = 0
k - 2k - 3k = - 1 - 4 + 6 - 12 - 9
- 4k = - 20
4k = 20
k = 5.
Esercizio 2:
dato il fascio di circonferenze di equazione x2 + y2 + 4x - y + k(x2 + y2 - 2x) = 0 dire per quali valori di k si ottiene l'equazione della circonferenza del fascio con centro sull'asse delle y.
Se il centro della circonferenza si trova sull'asse delle ordinate esso ha come ascissa il valore 0. In altre parole
C (0; β).
Andiamo a scrivere l'equazione del fascio di circonferenze nella forma canonica. Avremo:
x2 + y2 + 4x - y + k(x2 + y2 - 2x) = 0
x2 + y2 + 4x - y + kx2 + ky2 - 2kx = 0
(1+k) · x2 + (1+k) · y2 + (4 - 2k) · x - y = 0
Noi sappiamo che
-2α = a
ma poiché
α = 0
avremo che
a = 0.
Nella nostra equazione del fascio di circonferenze
a = 4 - 2k
quindi
4 - 2k = 0
- 2k = - 4
2k = 4
k = 2.
Esercizio 3:
dato il fascio di circonferenze di equazione x2 + y2 + kx - 2y - 2 = 0 dire per quali valori di k si ottiene l'equazione della circonferenza del fascio con centro sulla bisettrice del primo e terzo quadrante.
La bisettrice del primo e terzo quadrante è una retta la cui equazione è
y = x.
Se il centro della circonferenza da noi cercata deve trovarsi su questa retta, avremo necessariamente che l'ascissa e l'ordinata del centro devono essere uguali, ovvero
α = β.
Di conseguenza
-2α = -2β
e quindi
a = b.
L'equazione della nostra circonferenza è scritta in forma canonica
x2 + y2 + kx - 2y - 2 = 0.
Allora osserviamo che
a = k
b = -2.
Poiché
a = b
si avrà:
k = -2.
Esercizio 4:
dato il fascio di circonferenze x2 + y2 -6x - 4y + 9 + k(x2 + y2 - 14x - 4y + 49) = 0 determinare i punti base del fascio e l'asse radicale.
Le equazioni delle circonferenze generatrici del fascio sono:
x2 + y2 -6x - 4y + 9 = 0
e
x2 + y2 - 14x - 4y + 49 = 0.
Passiamo a trovare l'asse radicale mettendo a sistema le due circonferenze e applicando il metodo di riduzione
8x - 40 = 0.
Da cui otteniamo
8x = 40
x = 5
E abbiamo trovato l'asse radicale.
Ora mettiamo a sistema l'equazione della prima circonferenza generatrice con l'asse radicale.
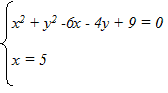
Sostituiamo nella prima la seconda ed abbiamo:
52 + y2 -6 · 5 - 4y + 9 = 0
25 + y2 - 30 - 4y + 9 = 0
y2 - 4y + 4 = 0.
Applichiamo la formula risolutiva:

Vi è un solo punto base, quindi ci troviamo di fronte ad un fascio di circonferenze tangenti e il punto di tangenza è
P(5; 2).






