ASSE RADICALE DI DUE CIRCONFERENZE
- Equazione della circonferenza
- Posizioni reciproche di due circonferenze
- Punti in comune a due circonferenze
- Equazione della retta: forma esplicita e forma implicita
- Principio di sostituzione di un sistema
- Rette perpendicolari
Nella lezione precedente abbiamo visto che, per trovare gli eventuali PUNTI IN COMUNE a DUE CIRCONFERENZE non concentriche mettiamo a sistema le equazioni delle due circonferenze. Successivamente, per poter risolvere il sistema, sottraiamo membro a membro in modo da ottenere:
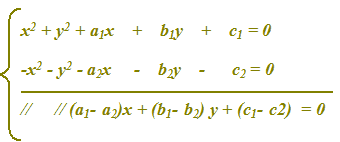
L'equazione ottenuta da questa sottrazione viene poi messa a sistema con l'equazione di una delle due circonferenze in modo da trovare le soluzioni del sistema stesso.
Ora soffermiamoci ad osservare l'equazione ottenuta
(a1 - a2)x + (b1 - b2)y + (c1 - c2) = 0.
Cerchiamo di capire cosa rappresenta questa equazione.
Innanzitutto osserviamo che si tratta di una equazione di primo grado del tipo
ax + by + c = 0.
Quindi possiamo dire che essa è l'equazione di una retta. Questa retta viene chiamata ASSE RADICALE.
Cerchiamo di capire di che retta si tratta.
Mettendo a sistema le equazioni delle due circonferenze noi andiamo a cercare i punti comuni ad entrambe. Applicando il principio di riduzione otteniamo un sistema equivalente a quello dato. Di conseguenza, la RETTA scritta, PASSA per gli eventuali PUNTI in COMUNE delle due circonferenze.
Vediamo cosa significa, questo, da un punto di vista grafico.
Se le due circonferenze sono SECANTI avremo:
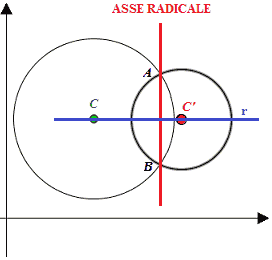
L'ASSE RADICALE passa per i punti A e B in comune alla due circonferenze. Cioè significa che esso è PERPENDICOLARE alla RETTA passante per i due CENTRI C e C', che nel grafico abbiamo disegnato in blu ed indicato con r.
Ovviamente, le due circonferenze secanti si sarebbero potute presentare anche in modo diverso, ad esempio:
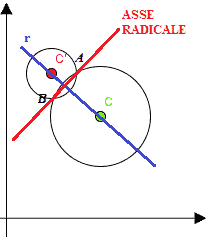
Se le due circonferenze sono TANGENTIi, avremo:
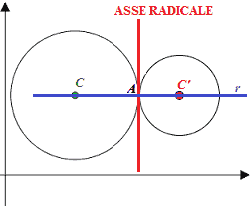
Cioè significa che l'ASSE RADICALE è la retta passante per il PUNTO di TANGENZA A delle due circonferenze.
Osserviamo che anche in questo caso l'ASSE RADICALE è PERPENDICOLARE alla RETTA passante per i due CENTRI C e C', che nel grafico abbiamo disegnato in blu ed indicato con r.
Ovviamente, anche in questo caso le due circonferenze tangenti si sarebbero potute presentare in modo diverso, ad esempio:
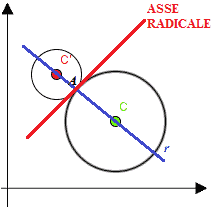
Quindi, concludendo possiamo dire che l'ASSE RADICALE di due circonferenze è la retta PERPENDICOLARE alla RETTA passante per i due CENTRI.
Per determinare l'equazione dell'ASSE RADICALE è sufficiente sottrarre, membro a membro, dall'equazione della prima circonferenza, quella della seconda circonferenza.
Nella prossima lezione vedremo come è possibile costruire graficamente l'asse radicale di due circonferenze che non siano secanti o tangenti.






