EQUAZIONE DELLA CIRCONFERENZA CONOSCENDO GLI ESTREMI DEL DIAMETRO
- Equazione della circonferenza
- Equazione della circonferenza: alcune considerazioni
- Equazione della circonferenza dati il centro e il raggio
- Distanza tra due punti sul piano
- Punto medio di un segmento
In questa lezione vogliamo capire come possiamo trovare l'EQUAZIONE DELLA CIRCONFERENZA quando conosciamo gli ESTREMI del suo DIAMETRO.
Immaginiamo che una circonferenza abbia come estremi del diametro i punti
A (x1; y1)
B (x2; y2).

In altre parole, noi conosciamo le coordinate di A e le coordinate di B.
Come possiamo notare facilmente, dal grafico riportato sopra, il CENTRO C non è altro che il PUNTO MEDIO del segmento AB.
Quindi dobbiamo trovare il segmento AB, in altre parole la distanza tra due punti, usando la formula
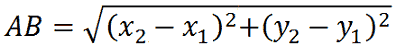
Successivamente possiamo trovare il suo punto medio usando la formula
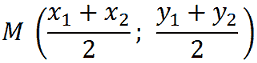
In questo modo avremo trovato le coordinate del centro C.
Inoltre il RAGGIO non è altro che la metà del diametro.
Quindi possiamo trovare il raggio dividendo il segmento AB per 2.
A questo punto ci troveremo a risolvere un problema nel quale dobbiamo scrivere l'EQUAZIONE della CIRCONFERENZA conoscendo il RAGGIO ed il CENTRO e basterà applicare la formula
(x - α)2 + (y - β)2 = r2.
Vediamo come procedere con un caso concreto.
Esempio:
scrivere l'equazione della circonferenza sapendo che un suo diametro ha per estremi i punti A(-1; 0) e B(3; 4).
Iniziamo col trovare il diametro della circonferenza, cioè la distanza tra A e B.
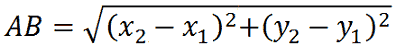

Ora cerchiamo le coordinate del centro, cioè il punto medio di A e B:
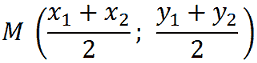

C (1; 2).
Il raggio della circonferenza è pari a:
r = 5,66 : 2 = 2,83.
Quindi scriviamo l'equazione della circonferenza applicando la formula
(x - α)2 + (y - β)2 = r2.
Noi sappiamo che
α = 1
β = 2
r = 2,83.
Quindi avremo:
(x - 1)2 + (y - 2)2 = 2,832
x2 + 1 - 2x + y2 + 4 - 4y = 8
x2 + y2 - 2x - 4y - 3 = 0.






