ELLISSE TRASLATA
Fin qui ci siamo occupati dell'ellisse canonica, ovvero dell'ellisse avente centro di simmetria nell'origine degli assi cartesiani e con gli assi di simmetria che coincidono con gli assi cartesiani:
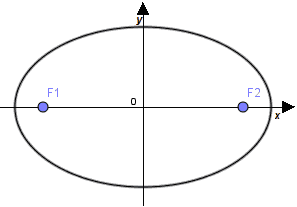
Chiaramente l'ellisse può anche avere un centro di simmetria diverso dall'origine degli assi. Si parla, in questi casi, di ELLISSE TRASLATA.
Un'ELLISSE si dice TRASLATA quando i suoi ASSI DI SIMMETRIA sono PARALLELI rispetto agli ASSI CARTESIANI.
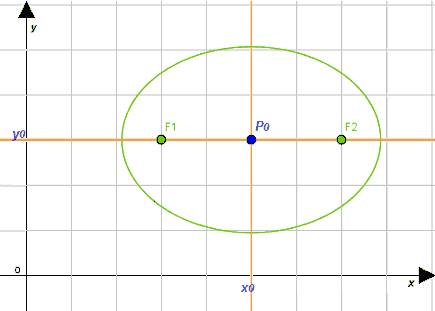
Nell'immagine che segue abbiamo disegnato un'ellisse traslata. Come possiamo notare gli assi di simmetria, disegnati in arancio, sono paralleli rispetto agli assi cartesiani e il centro di simmetria P0 non si trova nell'origine degli assi.
Supponiamo che le coordinate del punto P0 siano
P0 (x0 ; y0)
Ora ci poniamo il problema di trovarel'EQUAZIONE dell'ELLISSE TRASLATA.
Andiamo ad indicare con X e Y gli assi aventi per origine il punto P0 . Essi non sono altro che gli assi di simmetria della nostra ellisse:
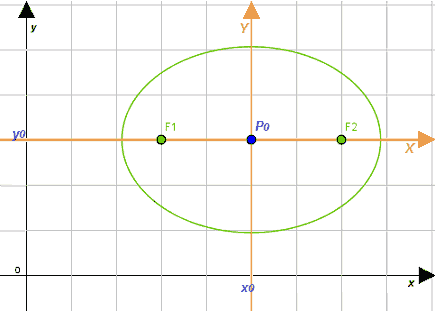
L'ellisse, quindi, risulta essere un'ellisse canonica rispetto al sistema di assi XP0 Y. Di conseguenza, possiamo dire che la nostra ellisse ha, rispetto al sistema di assi XP0 Y, un'equazione della forma
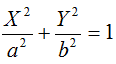
Ora noi vogliamo sapere quale forma assume la nostra equazione sul sistema iniziale di assi xOy.
Si tratterà, allora, di applicare le equazioni che ci permettono di passare alle coordinate del sistema xOy. Queste equazioni sono:
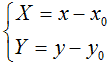
Effettuando le opportune sostituzioni avremo:
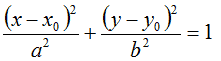
Quindi, questa è l'EQUAZIONE dell'ELLISSE TRASLATA, dove:
- x0 e y0 sono le coordinate del CENTRO dell'ellisse;
- a e b sono i due SEMIASSI dell'ellisse.
Nella prossima lezione vedremo come applicare questa equazione nella soluzione di alcuni esercizi.






