EQUAZIONE DELL'ELLISSE TRASLATA DATO IL CENTRO
Nella lezione precedente abbiamo visto che l'EQUAZIONE dell'ELLISSE TRASLATA è
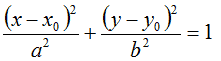
dove x0 e y0 rappresentano le coordinate del CENTRO.
Vediamo ora come possiamo trovare l'equazione dell'ellisse traslata se conosciamo le coordinate del centro.
Esempio:
scrivere l'equazione dell'ellisse con asse maggiore 10 e fuochi
F1 (-2; 3)
F2 (-2;-3).
Per poter scrivere l'equazione dell'ellisse traslata abbiamo bisogno:
- delle coordinate del centro x0 e y0;
- del valore dei semiassi a e b.
Noi non sappiamo le coordinate del centro, ma sappiamo che i fuochi hanno coordinate
F1 (-2; 3)
F2 (-2;-3).
Graficamente abbiamo:

Com'è noto i fuochi sono equidistanti dal centro, quindi il centro P0 ha come coordinate:
P0 (-2; 0).
Come possiamo notare dal grafico, i fuochi sono disposti sulla retta x = -2, quindi l'asse maggiore è 2b.
Noi sappiamo che
2b = 10
da cui otteniamo
b = 5
b2 = 25.
Ora, dato che conosciamo il valore di c, ci calcoliamo il valore di b2 applicando la relazione:
c2 = b2 - a2
(3)2 = 25 - a2
9 = 25 - a2
a2 = 25 - 9 = 16
Sostituiamo i valori ottenuti, nell'equazione dell'ellisse traslata:

Abbiamo così risolto il nostro problema.






