EQUAZIONE DELL'ELLISSE DATA L'ECCENTRICITA' ED UN PUNTO
- L'ellisse
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle x
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle y
- Sistemi di equazioni di secondo grado
In questa lezione vedremo, brevemente, come si può determinare l'EQUAZIONE di un'ELLISSE quando conosciamo la sua ECCENTRICITA' e le coordinate di un PUNTO per il quale essa passa.
Ipotizziamo che:
e = k
P (x1; y1).
Per poter risolvere questo tipo di problemi è però necessario sapere anche se i fuochi sono situati sull'asse delle ascisse o su quello delle ordinate.
Vediamo come occorre procedere.
Per prima cosa sostituiamo, all'equazione canonica dell'ellisse
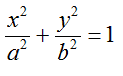
le coordinate del punto P in modo da trovare il valore dell'equazione quando passa per tale punto. Essa sarà:

Noi conosciamo l'eccentricità e sappiamo che
e = c/a - in cui i fuochi sono situati sull'asse delle ascisse
e = c/b - nel caso in cui i fuochi sono situati sull'asse delle ordinate.
Per questo è importante che il problema ci dica su quale asse si trovano i fuochi, in modo che noi sappiamo quale delle due relazioni considerare.
Inoltre noi sappiamo che
c2 = a2 -b2- nel caso in cui i fuochi sono situati sull'asse delle ascisse
c2 = b2 -a2- nel caso in cui i fuochi sono situati sull'asse delle ordinate.
Ora, elevando entrambi i membri nella formula dell'eccentricità, possiamo scrivere che:
e2 = c2/a2 - nel caso in cui i fuochi sono situati sull'asse delle ascisse
>e2 = c2/b2 - nel caso in cui i fuochi sono situati sull'asse delle ordinate.
Da cui sostituendo a numeratore il valore di c2, avremo:
e2 = (a2 - b2)/a2 - nel caso in cui i fuochi sono situati sull'asse delle ascisse
>e2 = (b2 - a2)/b2 - nel caso in cui i fuochi sono situati sull'asse delle ordinate.
Ma poiché il problema ci dice che
e = k
possiamo scrivere che
e2 = k2
e di conseguenza:
k2 = (a2 - b2)/a2 - nel caso in cui i fuochi sono situati sull'asse delle ascisse
k2 = (b2 - a2)/b2 - nel caso in cui i fuochi sono situati sull'asse delle ordinate.
A questo punto si tratterà di risolvere un sistema formato:
- dall'equazione dell'ellisse passante
per il punto P,
ovvero

- da una delle due formule
dell'eccentricità, a seconda di dove sono situati i fuochi.
Cioè:
k2 = (a2 - b2)/a2 - nel caso in cui i fuochi sono situati sull'asse delle ascisse
k2 = (b2 - a2)/b2 - nel caso in cui i fuochi sono situati sull'asse delle ordinate.
A questo punto si tratta solamente di risolvere il sistema nei modi consueti.






