EQUAZIONE DELL'ELLISSE CON CENTRO NELL'ORIGINE E FUOCHI SULL'ASSE DELLE Y
- L'ellisse
- Elementi dell'ellisse
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle x
- Il punto
- Distanza tra due punti sul piano
- Elevamento a potenza
- Raccoglimento a fattor comune
- L'insieme dei numeri reali
- Simboli usati per l'insieme dei numeri reali
- Caratteristiche dei triangoli
Osserviamo l'ELLISSE disegnata sotto:
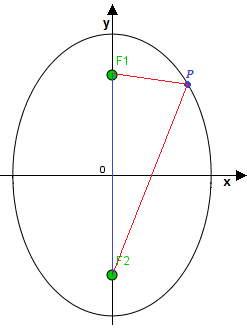
Come possiamo notare il CENTRO dell'ellisse è l'ORIGINE DEGLI ASSI, ma i FUOCHI, a differenza di quanto abbiamo visto nelle lezioni precedenti, si trovano sull'ASSE delle y.
Ora vogliamo dimostrare che l'EQUAZIONE di questa ellisse è la stessa di quella avente centro nell'origine degli assi e fuochi sull'asse delle x.
Partiamo dai due FUOCHI, F1 e F2, tali che:
F1 (0; c);
F2 (0; -c).
Prendiamo un generico P sull'ellisse
P (x; y).
Poiché l'ELLISSE è il luogo geometrico dei PUNTI del piano tali che la SOMMA delle DISTANZE da DUE PUNTI FISSI, detti FUOCHI, è COSTANTE, possiamo scrivere:
PF1 + PF2 = costante.
Ora poniamo la nostra COSTANTE uguale
a 2b. Possiamo
scrivere:
PF1 + PF2 = 2b.
Calcoliamo la distanza PF1:
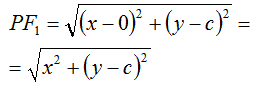
Ed ora calcoliamo la distanza PF2:
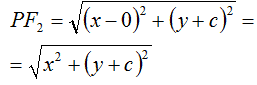
Quindipossiamo scrivere
PF1 + PF2 = 2b
nel modo seguente:
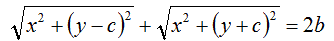
Portiamo a secondo membro il secondo radicale cambiando di segno:
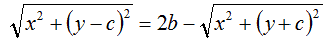
A questo punto eleviamo al quadrato primo e secondo membro
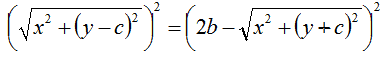
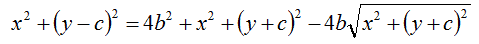
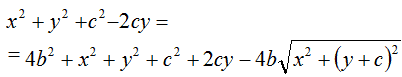
Andiamo a semplificare:
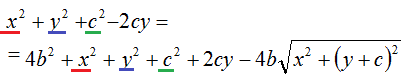
ottenendo:
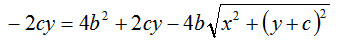
Isoliamo il radicale portandolo a primo membro e cambiandogli il segno:
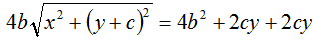
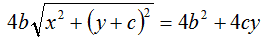
Ora, a secondo membro, andiamo a mettere in evidenza il 4:
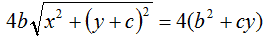
Dividiamo entrambi i membri per 4:
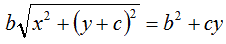
Andiamo ad elevare al quadrato il primo e il secondo membro:
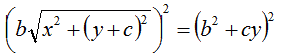
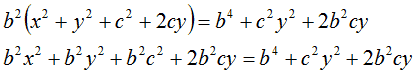
Semplifichiamo:
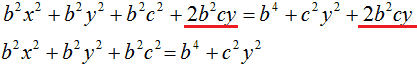
Portiamo a primo membro, cambiando di segno, c2y2, mentre portiamo a secondo membro, sempre cambiando di segno, b2c2. Otteniamo:
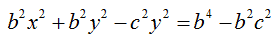
Ora mettiamo in evidenza, a primo membro y2, e a secondo membro b2. Avremo:
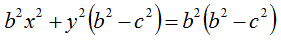
Poniamo
b2 - c2 = a2.
Tale sostituzione è possibile perché esiste sempre un valore di a appartenente all'insieme dei reali positivi R+ tali che
b2 - c2 = a2 .
Vediamone il perché.
Disegniamo il punto P appartenente all'ellisse e i fuochi F1 e F2:
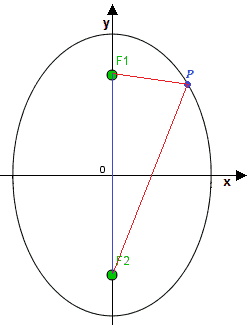
I segmenti PF1, PF2, F1F2 sono i lati di un TRIANGOLO.
Indichiamo la lunghezza del segmento F1F2 con 2c, ovvero
F1F2 = 2c.
Ora, noi sappiamo che in un TRIANGOLO OGNI LATO è sempre MINORE della SOMMA DEGLI ALTRI DUE.
Quindi possiamo scrivere:
F1F2 < PF1 +PF2 .
Ma poiché
F1F2 = 2c
e
PF1 +PF2 = 2b
possiamo dire che
2c < 2b
ovvero
c < b
quindi
c2 < b2
da cui
c2 - b2 < 0
ovvero
b2 - c2 > 0.
Quindi ci sarà sempre un valore di a appartenente all'insieme dei reali positivi R+ tale che
b2 - c2 = a2 .
Ora, torniamo alla nostra equazione, ed effettuiamo la sostituzione detta. Avremo:
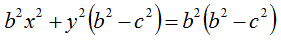
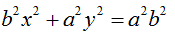
Andiamo a dividere entrambi i membri per a2b2:
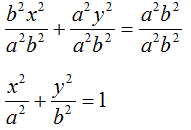
Quindil'EQUAZIONE DELL'ELLISE con CENTRO nell'ORIGINE degli assi e FUOCHI sull'ASSE delle y è la stessa che abbiamo visto nelle lezioni precedenti quando abbiamo parlato dell'equazione dell'ellisse con centro nell'origine degli assi e fuochi sull'asse delle x.
Anche in questo caso, come abbiamo già detto parlando dell'ellisse con fuochi sull'asse delle x, poiché gli ASSI di SIMMETRIA coincidono con gli ASSI CARTESIANI si parla di ELLISSE CANONICA.






