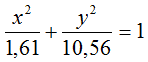EQUAZIONE DELL'ELLISSE DATI UN VERTICE ED UN PUNTO
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- L'ellisse
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle x
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle y
In questa lezione vedremo come si può determinare l'EQUAZIONE di un'ELLISSE quando conosciamo le coordinate di un suo VERTICE e di un PUNTO per il quale essa passa.
Esempio:
scrivere l'equazione canonica dell'ellisse con vertice
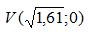
e passante per il punto
P (1; -2).
Sappiamo che l'equazione dell'ellisse nella sua forma canonica è
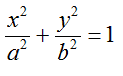
Quando l'ellisse passa per il punto V assume i seguenti valori:
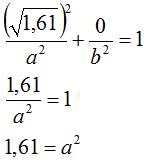
Così abbiamo trovato il valore di a2.
Quando l'ellisse passa per il punto P assume i seguenti valori:
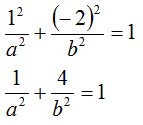
Sostituendo il valore già trovato di a2 avremo:
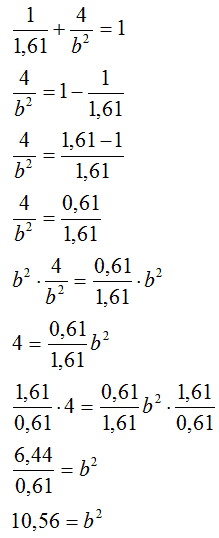
In questo modo abbiamo trovato anche il valore di b2.
Quindi l'equazione dell'ellisse sarà:
