ASSE MINORE DELL'ELLISSE
- L'ellisse
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle x
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle y
- Triangoli
- Figure geometriche equivalenti e figure geometriche congruenti
- Primo criterio di congruenza dei triangoli
- Gli angoli
- Angolo retto - angolo acuto - angolo ottuso
- Il segmento
- Distanza tra due punti aventi la stessa ascissa
- Le formule inverse del teorema di Pitagora
Nelle lezioni precedenti abbiamo detto che
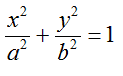
è l'EQUAZIONE DELL'ELLISE con CENTRO nell'ORIGINE degli assi e FUOCHI sull'ASSE delle y.
Data la nostra ellisse.
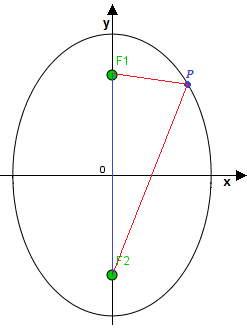
Sappiamo che i fuochi hanno coordinate
F1 (0; c)
F2 (0; -c).
e che l'asse maggiore è pari a 2b.
Ora vogliamo sapere a quanto è pari l'ASSE MINORE.
Prendiamo, il punto P tale che esso sia il PUNTO DI INTERSEZIONE dell'ELLISSE con il SEMIASSE POSITIVO delle x:

Ora tracciamo i segmenti PF1 e PF2

e osserviamo i triangoli PF2O e PF1O.

Il primo criterio di congruenza dei triangoli, ci dice che DUE TRIANGOLI sono CONGRUENTI se hanno rispettivamente CONGRUENTI:
- DUE LATI
- l'ANGOLO TRA ESSI COMPRESO.
Nel nostro caso il latoPO è comune ad entrambi i triangoli e dunque congruente.
Inoltre il lato OF1 è congruente con il lato OF2 dato che i FUOCHI sono EQUIDISTANTI dal CENTRO dell'ellisse.
L'angolo compreso tra il lato PO e il lato OF1 del primo triangolo è congruente con l'angolo compreso tra il lato PO e il lato OF2 del secondo triangolo, dato che entrambi sono angoli retti.
Quindi possiamo dire che i triangoli PF2O e PF1O sono CONGRUENTI. Di conseguenza il segmento PF1 e il segmento PF2 sono congruenti. Quindi possiamo scrivere:
PF1 = PF2
Ora, poiché noi sappiamo che
PF1 + PF2= 2b
e dato che
PF1 = PF2
possiamo scrivere che
PF1 + PF1 = 2b
ovvero
2PF1 = 2b
da cui
PF1 = b
e poiché
PF1 = PF2
sarà anche
PF2 = b.
Ora vogliamo trovare la misura del segmento F1F2 che sappiamo essere la distanza focale. Come sappiamo la distanza tra due punti A e B tali che
A (x; y1)
B(x; y2)
è data da
AB = |y2 - y1|.
Le coordinate dei due fuochi sono
F1 (0; c)
F2 (0; -c)
Quindi la DISTANZA FOCALE, ovvero la distanza tra i due fuochi, è uguale a:
F1F2 = |c + c| = |2c| = 2c.
Quindi possiamo dire che il segmento
OF2 = 2c/2 = c.
A questo punto, applicando il TEOREMA DI PITAGORA, siamo in grado di determinare la misura del segmento OP. Ovvero:

Ora, ricordando che, nello scrivere l'equazione dell'ellisse abbiamo posto
b2 - c2 = a2
possiamo sostituire ed ottenere

Il segmento OP, da noi trovato, è il semiasse minore.

Poiché l'ASSE MINORE ha un valore doppio rispetto al semiasse minore, esso sarà pari a 2a.
Ricapitolando i valori trovati:







