DISEQUAZIONI FRATTE CON VALORE ASSOLUTO A NUMERATORE O A DENOMINATORE
- Disequazioni fratte
- Disequazioni con valore assoluto
- Disequazioni fratte con valore assoluto
- Disequazioni fratte con valore assoluto
- Disequazioni fratte con valore assoluto a numeratore o a denominatore
Con questa lezione concludiamo l'esame delle DISEQUAZIONI FRATTE con VALORE ASSOLUTO.
Ora ci occuperemo delle disequazioni che si presentano in una delle forme seguenti:
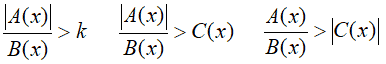
Ovviamente, nulla cambia in quello che diremo:
- se, anziché il segno di maggiore troviamo il segno di maggiore uguale o minore o minore uguale;
- se, nei primi due casi, il valore assoluto si trova a denominatore anziché a numeratore.
Il modo di procedere, in tutti e tre i casi, è sempre lo stesso: PORTIAMO, tutto quello che si trova a secondo membro, a PRIMO MEMBRO e lo scriviamo all'INTERNO della FRAZIONE moltiplicandolo per il MINIMO COMUNE DENOMINATORE.
Poi risolviamo secondo le regole che abbiamo appreso nelle lezioni precedenti ricordando sempre che, trattandosi di frazioni, dovremo studiare il segno del numeratore e del denominatore.
Esempio:
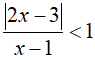
Portiamo l'1 a primo membro cambiandogli di segno:
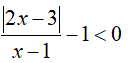
Quindi lo portiamo nella frazione dopo averlo moltiplicato per il minimo comune denominatore:
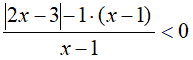
Sviluppiamo:
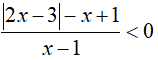
Studiamo, separatamente, il segno del numeratore e del denominatore.
NUMERATORE:
|2x - 3| - x +1 ≥ 0.
Applichiamo la regola dei segni appresa nella lezione 5 ponendo l'espressione presente all'interno del modulo maggiore o uguale a zero:
2x - 3 ≥ 0
2x ≥ 3
x ≥ 3/2.
Quindi, quando la x è minore di 3/2, l'espressione all'interno del modulo è negativa e il sistema da risolvere è:
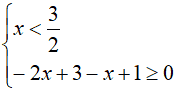
Quando la x è maggiore o uguale a 3/2, l'espressione all'interno del modulo è positiva o nulla e il sistema da risolvere è:
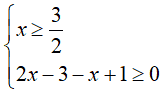
1° SISTEMA
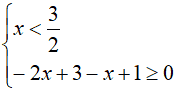
Risolviamo la seconda disequazione:
- 2x + 3 - x + 1 ≥ 0
- 3x + 4 ≥ 0
3x - 4 ≤ 0
3x ≤ 4
x ≤ 4/3.
La soluzione del sistema è

x ≤ 4/3
2° SISTEMA
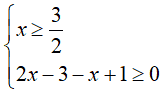
Risolviamo la seconda disequazione:
2x - 3 - x + 1 ≥ 0
x - 2 ≥ 0
x ≥ 2.
La soluzione del sistema è

x ≥ 2.
Quindi il NUMERATORE è POSITIVO quando
x ≤ 4/3 ˅ x ≥ 2.
DENOMINATORE:
x - 1 ≥ 0
x ≥ 1.
STUDIAMO IL SEGNO DELLA FRAZIONE
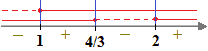
A noi interessa sapere quando la nostra disequazione è negativa. Ciò accade quando
x < 1 ˅ 4/3 < x <2.
Un altro tipo di disequazione frazionaria con valore assoluto che potremmo incontrare è:
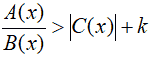
In questo caso portiamo solamente k a primo membro e lo scriviamo nella frazione dopo averlo moltiplicato per il minimo comune denominatore:
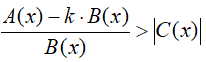
La disequazione può essere scritta anche nel modo seguente:
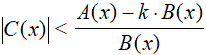
Essa si risolve allo stesso modo delle disequazioni del tipo:
|A(x)| < B(x)
di cui abbiamo già avuto modo di parlare nella lezione 6 a cui si rimanda.






